题目内容
13.计算:(1)$\sqrt{121}$-10-1+$\root{3}{27}$-5sin30°+(3.14-π)0
(2)已知m2-5=3m,求代数式2m2-6m-1的值.
分析 (1)原式利用算术平方根、立方根定义,零指数幂、负整数指数幂法则,以及特殊角的三角函数值计算即可得到结果;
(2)原式变形后,将已知等式整理代入计算即可求出值.
解答 解:(1)原式=11-0.1+3-2.5+1=12.4;
(2)∵m2-5=3m,即m2-3m=5,
∴原式=2(m2-3m)-1=10-1=9.
点评 此题考查了实数的运算,零指数幂、负整数指数幂,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
3.在一个不透明的口袋中装有4个红球和若干个白球,它们除颜色外其他完全相同.通过多次摸球试验后发现,摸到红球的频率稳定在25%附近,则口袋中白球可能有( )
| A. | 13个 | B. | 12个 | C. | 16个 | D. | 15个 |
4.某天的最高气温是5℃,最低气温是-4℃,则这一天气温的温差是( )
| A. | 1℃ | B. | -1℃ | C. | 9℃ | D. | -9℃ |
1.若代数式$\frac{\sqrt{x+1}}{x-2}$在实数范围内有意义,则实数x的取值范围是( )
| A. | x≥-1 | B. | x>2 | C. | x≠2 | D. | x≥-1且x≠2 |
18.-2017的相反数是( )
| A. | ±2017 | B. | -2017 | C. | 2017 | D. | -2018 |
5.某体校要从四名射击选手中选拔一名参加体育运动会,选拔赛中每名选手连续射靶10次,他们各自的平均成绩及其方差s2如表所示,如果要选出一名成绩高,且发挥稳定的选手参赛,则应选择的选手是乙.
| 甲 | 乙 | 丙 | 丁 | |
| $\overline{x}$(环) | 8.4 | 8.6 | 8.6 | 7.6 |
| S2 | 0.74 | 0.56 | 0.94 | 1.92 |
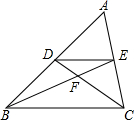 如图,在任意△ABC中,DE∥BC,连接BE与CD相交于点F,则下列结论一定正确的有几个( )
如图,在任意△ABC中,DE∥BC,连接BE与CD相交于点F,则下列结论一定正确的有几个( ) 如图,AB∥CD,∠DCE=118°,∠AEC的角平分线EF与GF相交于点F,∠BGF=132°,则∠F的度数是11°.
如图,AB∥CD,∠DCE=118°,∠AEC的角平分线EF与GF相交于点F,∠BGF=132°,则∠F的度数是11°.