题目内容
9.已知△ABC中,∠B-∠A=70°,∠C=50°,求∠A、∠B的度数.分析 根据三角形内角和定理可得∠A+∠B=130°,再联立条件∠B-∠A=70°,解方程组即可.
解答 解:∵∠C=50°,
∴∠A+∠B=130°,
∵∠B-∠A=70°,
∴∠B=100°,∠A=30°.
点评 此题主要考查了三角形内角和定理,关键是掌握三角形内角和是180°.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
17.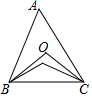 在如图所示的锐角三角形ABC中,O是其外接圆圆心,I是其内切圆圆心,若∠BOC=∠BIC,则sinA的值是( )
在如图所示的锐角三角形ABC中,O是其外接圆圆心,I是其内切圆圆心,若∠BOC=∠BIC,则sinA的值是( )
 在如图所示的锐角三角形ABC中,O是其外接圆圆心,I是其内切圆圆心,若∠BOC=∠BIC,则sinA的值是( )
在如图所示的锐角三角形ABC中,O是其外接圆圆心,I是其内切圆圆心,若∠BOC=∠BIC,则sinA的值是( )| A. | $\frac{3}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
18.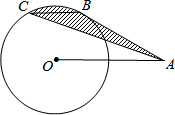 如图所示,A是半径为1的⊙O外的一点,OA=2,AB是⊙O的切线,B是切点,弦BC∥OA,连接AC,则阴影部分的面积等于( )
如图所示,A是半径为1的⊙O外的一点,OA=2,AB是⊙O的切线,B是切点,弦BC∥OA,连接AC,则阴影部分的面积等于( )
 如图所示,A是半径为1的⊙O外的一点,OA=2,AB是⊙O的切线,B是切点,弦BC∥OA,连接AC,则阴影部分的面积等于( )
如图所示,A是半径为1的⊙O外的一点,OA=2,AB是⊙O的切线,B是切点,弦BC∥OA,连接AC,则阴影部分的面积等于( )| A. | $\frac{2π}{9}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{6}+\frac{\sqrt{3}}{8}$ | D. | $\frac{π}{4}-\frac{\sqrt{3}}{8}$ |
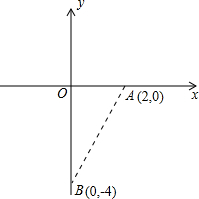 在直角坐标系中,以点A(2,0)为圆心作圆,使圆经过点B(0,-4),如图所示,试判断C(0,4)、D(-2,0)、E(0,8)与⊙A的位置关系.若点M(0,m)在⊙A外,求m的取值范围.
在直角坐标系中,以点A(2,0)为圆心作圆,使圆经过点B(0,-4),如图所示,试判断C(0,4)、D(-2,0)、E(0,8)与⊙A的位置关系.若点M(0,m)在⊙A外,求m的取值范围. 如图,已知?ABCD中,对角线AC与BD相交于点O,且AC=$\sqrt{2}$DC,求证:∠AOB=∠ADC.
如图,已知?ABCD中,对角线AC与BD相交于点O,且AC=$\sqrt{2}$DC,求证:∠AOB=∠ADC. 如图,已知点E是正方形ABCD的边BC上的一点,把线段AE绕点E顺时针旋转90°得到线段EF,连接CF,AF.
如图,已知点E是正方形ABCD的边BC上的一点,把线段AE绕点E顺时针旋转90°得到线段EF,连接CF,AF. 如图,已知EF是梯形ABCD的中位线,AH平分∠BAD交EF于点G,交BC于点H,若AB=10cm,AD=8cm,DC=4cm,求FG的长.
如图,已知EF是梯形ABCD的中位线,AH平分∠BAD交EF于点G,交BC于点H,若AB=10cm,AD=8cm,DC=4cm,求FG的长.