题目内容
17.在平面直角坐标系中,已知点E(-6,4),F(-3,-3),以原点O为位似中心,相似比为$\frac{1}{2}$,把△EFO缩小,则E点对应点E′的坐标是(3,-2)(-3,2).分析 根据在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k解答.
解答 解:∵点E(-6,4),以原点O为位似中心,相似比为$\frac{1}{2}$,把△EFO缩小,
∴点E′的坐标是(-6×$\frac{1}{2}$,4×$\frac{1}{2}$),即(-3,2),
(-6×(-$\frac{1}{2}$),4×(-$\frac{1}{2}$)),即(3,-2),
故答案为:(3,-2)(-3,2).
点评 本题考查的是位似变换的概念和性质,在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k.

练习册系列答案
相关题目
5.数1、0、$\frac{1}{2}$、-3、$-\frac{1}{5}$可以统称为( )
| A. | 整数 | B. | 分数 | C. | 负数 | D. | 有理数 |
9. 一副三角板有两个直角三角形,以如图所示的方式叠放在一起,则∠DFC的度数是( )
一副三角板有两个直角三角形,以如图所示的方式叠放在一起,则∠DFC的度数是( )
 一副三角板有两个直角三角形,以如图所示的方式叠放在一起,则∠DFC的度数是( )
一副三角板有两个直角三角形,以如图所示的方式叠放在一起,则∠DFC的度数是( )| A. | 165° | B. | 120° | C. | 150° | D. | 135° |
7.将两块长为am,宽为bm的长方形红布,加工成一个长为cm,宽为dm的长方形,有人就a,b,c,d的关系写出如下四个等式,不过他写错了一个,写错的那个是( )
| A. | $\frac{2a}{c}=\frac{d}{b}$ | B. | $\frac{a}{c}=\frac{d}{2b}$ | C. | $\frac{2a}{d}=\frac{c}{b}$ | D. | $\frac{a}{2c}=\frac{d}{b}$ |
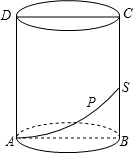 如图,在圆柱的截面ABCD中,AB=$\frac{16}{π}$,BC=12,动点P从A点出发,沿着圆柱的侧面移动到BC的中点S的最短距离为10.
如图,在圆柱的截面ABCD中,AB=$\frac{16}{π}$,BC=12,动点P从A点出发,沿着圆柱的侧面移动到BC的中点S的最短距离为10. 已知在纸面上有一数轴(如图),折叠纸面.例如:若数轴上数2表示的点与数-2表示的点重合,则数轴上数-4表示的点与数4表示的点重合,根据你对例题的理解,解答下列问题:
已知在纸面上有一数轴(如图),折叠纸面.例如:若数轴上数2表示的点与数-2表示的点重合,则数轴上数-4表示的点与数4表示的点重合,根据你对例题的理解,解答下列问题: