题目内容
8.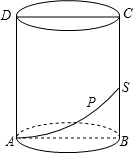 如图,在圆柱的截面ABCD中,AB=$\frac{16}{π}$,BC=12,动点P从A点出发,沿着圆柱的侧面移动到BC的中点S的最短距离为10.
如图,在圆柱的截面ABCD中,AB=$\frac{16}{π}$,BC=12,动点P从A点出发,沿着圆柱的侧面移动到BC的中点S的最短距离为10.
分析 先把圆柱的侧面展开,连接AS,利用勾股定理即可得出AS的长.
解答  解:如图所示,
解:如图所示,
∵在圆柱的截面ABCD中AB=$\frac{16}{π}$,BC=12,
∴AB=$\frac{1}{2}$×$\frac{16}{π}$×π=8,BS=$\frac{1}{2}$BC=6,
∴AS=$\sqrt{{8}^{2}+{6}^{2}}$=10.
故答案为:10.
点评 本题考查的是平面展开-最短路径问题,根据题意画出圆柱的侧面展开图,利用勾股定理求解是解答此题的关键.

练习册系列答案
相关题目
13.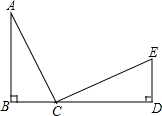 如图,已知AB⊥BD,ED⊥BD,AB=CD,AC=CE,则∠ACE等于( )
如图,已知AB⊥BD,ED⊥BD,AB=CD,AC=CE,则∠ACE等于( )
 如图,已知AB⊥BD,ED⊥BD,AB=CD,AC=CE,则∠ACE等于( )
如图,已知AB⊥BD,ED⊥BD,AB=CD,AC=CE,则∠ACE等于( )| A. | 90° | B. | 120° | C. | 80° | D. | 100° |
 作图:如图,平面内有A,B,C,D四点.按下列语句画图:
作图:如图,平面内有A,B,C,D四点.按下列语句画图: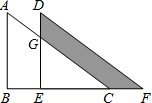 如图是重叠的两个直角三角形,将其中一个直角三角形沿BC方向平移得到三角形DEF,若AB=8cm,BE=4cm,DG=3cm,则图中阴影部分的面积是多少cm2?
如图是重叠的两个直角三角形,将其中一个直角三角形沿BC方向平移得到三角形DEF,若AB=8cm,BE=4cm,DG=3cm,则图中阴影部分的面积是多少cm2?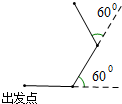 如图,小华在空旷的操场上向右行走20米后,接着向左转60°,再向前行走20米,再接着向左转,再向前行走20米,…这样一直走下去.
如图,小华在空旷的操场上向右行走20米后,接着向左转60°,再向前行走20米,再接着向左转,再向前行走20米,…这样一直走下去.