Question

18．矩形ABCD中，E是CD上一点，且AE=CE，F是AC上一点FH⊥AE于H，FG⊥CD于G，求证：FH+FG=AD．

Answer 1

分析 连接EF，由△ACE的面积=△AEF的面积+△CEF的面积=$\frac{1}{2}$AE•FH+$\frac{1}{2}$CE•FG，△ACE的面积=$\frac{1}{2}$CE•AD，再由AE=CE，即可得出结论．

解答 证明：连接EF，如图所示：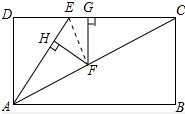
∵FH⊥AE于H，FG⊥CD于G，
∴△ACE的面积=△AEF的面积+△CEF的面积=$\frac{1}{2}$AE•FH+$\frac{1}{2}$CE•FG，
∵AE=CE，
∴△ACE的面积=$\frac{1}{2}$CE（FH+FG），
又∵四边形ABCD是矩形，
∴AD⊥CD，
∴△ACE的面积=$\frac{1}{2}$CE•AD，
∴FH+FG=AD．

点评 本题考查了矩形的性质、三角形面积的计算方法；熟练掌握矩形的性质和三角形面积的计算，作出辅助线是解决问题的关键．