题目内容
12．
有许多代数恒等式可以用图形的面积来表示，如图①，它表示（2m+2n）（m+n）=2m2+3mn+n2．观察图②，请你写出三个代数式（m+n）2、（m-n）2、mn之间的等量关系是（m+n）2-4mn=（m-n）2；（m+n）2-（m-n）2=4mn；（m-n）2+4mn=（m+n）2．
分析 大正方形的面积减去矩形的面积即可得出阴影部分的面积，可得出三个代数式（m+n）2、（m-n）2、mn之间的等量关系；依此即可求解．
解答 解：观察图②可知，代数式（m+n）2、（m-n）2、mn之间的等量关系式：（m+n）2-4mn=（m-n）2；（m+n）2-（m-n）2=4mn；（m-n）2+4mn=（m+n）2．
故答案为：（m+n）2-4mn=（m-n）2；（m+n）2-（m-n）2=4mn；（m-n）2+4mn=（m+n）2．
点评 本题考查了完全平方公式的几何背景，属于基础题，注意仔细观察图形，表示出各图形的面积是关键．
练习册系列答案
相关题目
如图，在△ABC中，∠A=90°，∠ABC=60°，BD平分∠ABC，AC=12cm，则CD=8cm．
矩形ABCD中，E是CD上一点，且AE=CE，F是AC上一点FH⊥AE于H，FG⊥CD于G，求证：FH+FG=AD．
17．
如图，△ABC中，∠A=36°，AB=AC，BD平分∠ABC，下列结论错误的是（ ）
如图，△ABC中，∠A=36°，AB=AC，BD平分∠ABC，下列结论错误的是（ ）| A． | ∠C=2∠A | B． | BD=BC | ||
| C． | △ABD是等腰三角形 | D． | 点D为线段AC的中点 |
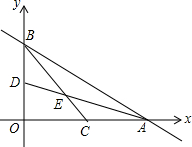如图，直线y=-$\frac{1}{2}$x+2交x轴于A点，交y轴于B点，C、D分别为OA、OB的中点，连接AD、BC相交于E点．