题目内容
已知一次函数y=(m+4)x-3+n(其中x是自变量).
(1)当m、n为何值时,函数图象与y轴的交点在x轴下方?
(2)当m,n为何值时,函数图象过原点,且y随x的增大而增大?
(3)当m,n为何值时,函数的图象平行于直线y=-x?
(1)当m、n为何值时,函数图象与y轴的交点在x轴下方?
(2)当m,n为何值时,函数图象过原点,且y随x的增大而增大?
(3)当m,n为何值时,函数的图象平行于直线y=-x?
考点:一次函数图象与系数的关系
专题:
分析:(1)要使函数图象与y轴的交点在x轴下方,则应使m+4≠0,-3+n<0,求解即可;
(2)要使函数图象过原点,且y随x的增大而增大,则应使m+4>0,-3+n=0,求解即可;
(3)要使函数图象平行于直线y=-x,则应使m+4=-1,-3+n≠0,求解即可.
(2)要使函数图象过原点,且y随x的增大而增大,则应使m+4>0,-3+n=0,求解即可;
(3)要使函数图象平行于直线y=-x,则应使m+4=-1,-3+n≠0,求解即可.
解答:解:(1)一次函数y=(m+4)x-3+n中令x=0,得到y=-3+n,
函数图象与y轴的交点在x轴下方得到-3+n<0,
解得n<3,
y=(m+4)x-3+n是一次函数,因而m+4≠0,
∴m≠-4,即当m、n为m≠-4,n<3时,函数图象与y轴的交点在x轴下方;
(2)当一次函数y=(m+4)x-3+n的图象过原点,且y随x的增大而增大,
∴m+4>0,-3+n=0,
解得:m>-4,n=3,
∴当m>-4,n=3时,函数图象过原点,且y随x的增大而增大;
(3)当一次函数y=(m+4)x-3+n的图象平行于直线y=-x,
∴m+4=-1,-3+n≠0,
解得:m=-5,n≠3,
∴当m=-5,n≠3时,函数图象平行于直线y=-x;
函数图象与y轴的交点在x轴下方得到-3+n<0,
解得n<3,
y=(m+4)x-3+n是一次函数,因而m+4≠0,
∴m≠-4,即当m、n为m≠-4,n<3时,函数图象与y轴的交点在x轴下方;
(2)当一次函数y=(m+4)x-3+n的图象过原点,且y随x的增大而增大,
∴m+4>0,-3+n=0,
解得:m>-4,n=3,
∴当m>-4,n=3时,函数图象过原点,且y随x的增大而增大;
(3)当一次函数y=(m+4)x-3+n的图象平行于直线y=-x,
∴m+4=-1,-3+n≠0,
解得:m=-5,n≠3,
∴当m=-5,n≠3时,函数图象平行于直线y=-x;
点评:本题考查了一次函数的图象与系数的关系,函数图象与y轴的交点在x轴下方,即函数值小于0,求出函数与y轴的交点是解决本题的关键.

练习册系列答案
相关题目
若二次根式
有意义,则x的取值范围是( )
| 2-x |
| A、x≥2 | B、x>2 |
| C、x≤2 | D、x<2 |
正方形内有一点P到各边的距离为2,3,4,5,则正方形的面积为( )
| A、36 | B、49 | C、64 | D、81 |
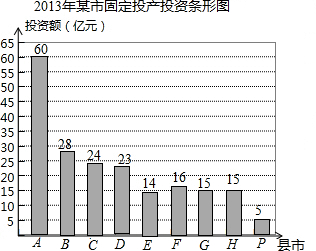 某地统计局对2013年各县市的固定资产投资情况进行了统计,并绘成了如图,请根据相关信息解答下列问题:下列结论不正确的是( )
某地统计局对2013年各县市的固定资产投资情况进行了统计,并绘成了如图,请根据相关信息解答下列问题:下列结论不正确的是( )| A、2013年某市固定资产投资总额为200亿元 |
| B、2013年某市各单位固定资产投资额的中位数是16亿元 |
| C、2013年A县固定资产投资额为占总额的30% |
| D、2013年固定资产投资扇形统计图中表示A地的扇形的圆心角为110° |
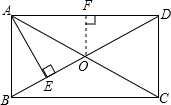 如图,在矩形ABCD中,对角线AC、BD交于点O,自点A作AE⊥BO于点E,且BE:ED=1:3,过点O作OF⊥AD于点F,若OF=3cm,求BD的长.
如图,在矩形ABCD中,对角线AC、BD交于点O,自点A作AE⊥BO于点E,且BE:ED=1:3,过点O作OF⊥AD于点F,若OF=3cm,求BD的长.