题目内容
如图,在?ABCD中,E、F为对角线BD上的两点.
(1)若AE⊥BD,CF⊥BD,证明BE=DF.
(2)若AE=CF,能否说明BE=DF?若能,请说明理由;若不能,请画出反例.
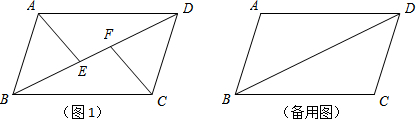
(1)若AE⊥BD,CF⊥BD,证明BE=DF.
(2)若AE=CF,能否说明BE=DF?若能,请说明理由;若不能,请画出反例.

考点:平行四边形的性质,全等三角形的判定与性质
专题:
分析:(1)证明△AEB≌△CFD,即可得出结论;
(2)画出图形说明即可.
(2)画出图形说明即可.
解答:解:(1)∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD,
在△AEB和△CFD中,
,
∴△AEB≌△CFD(AAS),
∴BE=DF.
(2)答:不能.
反例:
 .
.
∴∠AEB=∠CFD,
在△AEB和△CFD中,
|
∴△AEB≌△CFD(AAS),
∴BE=DF.
(2)答:不能.
反例:
 .
.点评:本题考查了平行四边形的性质,题目比较灵活,注意第二问举反例时,以AE(CF)为基础,寻找CF(AE),从而得出反例.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列哪一个数与方程x3-49=16的根最接近( )
| A、2 | B、3 | C、4 | D、5 |
若四个数2,x,3,5的中位数为4,则有( )
| A、x=4 | B、x=6 |
| C、x≥5 | D、x≤5 |
 如图,AB是⊙O的直径,CD为弦,CD⊥AB于点E,CD=16cm,BE=4cm,求⊙O的半径.
如图,AB是⊙O的直径,CD为弦,CD⊥AB于点E,CD=16cm,BE=4cm,求⊙O的半径.