题目内容
20.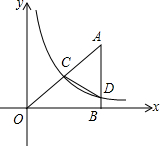 如图,在平面直角坐标系中,点A的横坐标为8,AB⊥x轴于点B,sin∠OAB=$\frac{4}{5}$,反比例函数y=$\frac{k}{x}$的图象的一支经过AO的中点C,交AB于点D.
如图,在平面直角坐标系中,点A的横坐标为8,AB⊥x轴于点B,sin∠OAB=$\frac{4}{5}$,反比例函数y=$\frac{k}{x}$的图象的一支经过AO的中点C,交AB于点D.(1)求反比例函数的解析式;
(2)四边形OCDB的面积.
分析 (1)先根据锐角三角函数的定义,求出OA的值,然后根据勾股定理求出AB的值,然后由C点是OA的中点,求出C点的坐标,然后将C的坐标代入反比例函数y=$\frac{k}{x}$中,即可确定反比例函数解析式;
(2)作CE⊥x轴于点E,然后根据S四边形OCDB=S△OCE+S梯形CEBD即可求解.
解答 解:(1)∵A点的坐标为(8,y),
∴OB=8,
∵AB⊥x轴于点B,sin∠OAB=$\frac{4}{5}$,
∴$\frac{OB}{OA}$=$\frac{4}{5}$,
∴OA=10,
由勾股定理得:AB=$\sqrt{O{A}^{2}-O{B}^{2}}$=6,
∵点C是OA的中点,且在第一象限内,
∴C(4,3),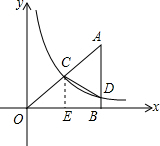
∵点C在反比例函数y=$\frac{k}{x}$的图象上,
∴k=12,
∴反比例函数解析式为:y=$\frac{12}{x}$;
(2)作CE⊥x轴于点E.则E的坐标是(4,0).
OE=BE=4,CE=3.
在y=$\frac{12}{x}$中,令x=8,解得y=$\frac{3}{2}$,则BD=$\frac{3}{2}$.
则S四边形OCDB=S△OCE+S梯形CEBD=$\frac{1}{2}$OE•CE+$\frac{1}{2}$(CE+BD)•BE=$\frac{1}{2}$×3×4+$\frac{1}{2}$(3+$\frac{3}{2}$)×4=6+9=15.
点评 本题考查了待定系数法求函数的解析式以及图形的面积的计算,在计算不规则的图形的面积时常用的方法是转化成规则图形的面积的和或差计算.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
10.迎接学校“元旦”文艺汇演,八年级某班的全体同学捐款购买了表演道具,经过充分的排练准备,最终获得了一等奖.班长对全体同学的捐款情况绘制成下表:
由于填表时不小心把墨水滴在了统计表上,致使表中数据不完整,但知道捐款金额为10元的人数为全班人数的30%,结合上表回答下列问题:
(1)该班共有50名同学;
(2)该班同学捐款金额的众数是15元,中位数是12.5元.
(3)如果把该班同学的捐款情况绘制成扇形统计图,则捐款金额为20元的人数所对的扇形圆心角为
36度.
| 捐款金额 | 5元 | 10元 | 15元 | 20元 |
| 捐款人数 | 10人 | 15人 |  | 5人 |
(1)该班共有50名同学;
(2)该班同学捐款金额的众数是15元,中位数是12.5元.
(3)如果把该班同学的捐款情况绘制成扇形统计图,则捐款金额为20元的人数所对的扇形圆心角为
36度.
5.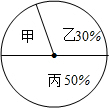 某学校学生来自甲、乙、丙三个地区,如图是甲、乙、丙三个地区学生人数的扇形统计图,已知来自甲地区的学生有180人,则下列说法不正确的是( )
某学校学生来自甲、乙、丙三个地区,如图是甲、乙、丙三个地区学生人数的扇形统计图,已知来自甲地区的学生有180人,则下列说法不正确的是( )
 某学校学生来自甲、乙、丙三个地区,如图是甲、乙、丙三个地区学生人数的扇形统计图,已知来自甲地区的学生有180人,则下列说法不正确的是( )
某学校学生来自甲、乙、丙三个地区,如图是甲、乙、丙三个地区学生人数的扇形统计图,已知来自甲地区的学生有180人,则下列说法不正确的是( )| A. | 甲对应扇形的圆心角为72° | B. | 学生的总人数是900人 | ||
| C. | 甲比丙地区人数少180人 | D. | 丙比乙地区人数多180人 |
 如图,点P是线段MN上一点,点Q是PN的中点,PQ=4cm,则MN-MP的长为8cm.
如图,点P是线段MN上一点,点Q是PN的中点,PQ=4cm,则MN-MP的长为8cm.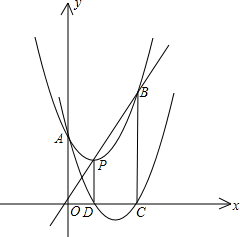 若将抛物线F:抛物线y=x2+bx$\frac{9}{2}$改成y=ax2+bx+c,抛物线的顶点为P,与y轴交于点A,与直线OP交于点B.过点P作PD⊥x轴于点D,平移抛物线F使其经过点A、D得到抛物线F′:y=a′x2+b′x+c′,抛物线F′与x轴的另一个交点为C.且a、b、c满足了b2=2ac
若将抛物线F:抛物线y=x2+bx$\frac{9}{2}$改成y=ax2+bx+c,抛物线的顶点为P,与y轴交于点A,与直线OP交于点B.过点P作PD⊥x轴于点D,平移抛物线F使其经过点A、D得到抛物线F′:y=a′x2+b′x+c′,抛物线F′与x轴的另一个交点为C.且a、b、c满足了b2=2ac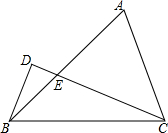 如图,在△ABC中,BC=2$\sqrt{2}$,∠ABC=45°=2∠ECB,BD⊥CD,则(2BD)2=16-8$\sqrt{2}$.
如图,在△ABC中,BC=2$\sqrt{2}$,∠ABC=45°=2∠ECB,BD⊥CD,则(2BD)2=16-8$\sqrt{2}$.