题目内容
2．若代数式（3x2-mx-3y+4）-（8nx2-x+2y-3）的值与字母x的取值无关，求代数式（-m2+2mn-n2）-2（mn-3m2）+3（2n2-mn）的值．分析 已知代数式去括号合并得到最简结果，由结果与x取值无关求出m与n的值，原式去括号合并后代入计算即可求出值．
解答 解：原式=3x2-mx-3y+4-8nx2+x-2y+3=（3-8n）x2+（1-m）x-5y+7，
由结果与x的取值无关，得到3-8n=0，1-m=0，
解得：m=1，n=$\frac{3}{8}$，
则原式=-m2+2mn-n2-2mn+6m2+6n2-3mn=5m2-3mn+5n2=5-$\frac{9}{8}$+$\frac{45}{64}$=5-$\frac{27}{64}$=4$\frac{37}{64}$．
点评 此题考查了整式的加减-化简求值，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
17．七年级一班和二班各组织了一个舞蹈队，一班舞蹈队有a人，平均身高为m米，二班舞蹈队有b人，平均身高为n米，这两个舞蹈队合起来组成了年级舞蹈队，那么年级舞蹈队的平均身高为（ ）
| A． | $\frac{m+n}{2}$ | B． | $\frac{a+b}{2}$ | C． | $\frac{am+bn}{m+n}$ | D． | $\frac{am+bn}{a+b}$ |
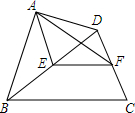如图，在四边形ABCD中，AD⊥AB，BD=BC，点E、F分别是边BD、CD的中点，∠ABD=34°，∠DBC=40°，求∠EAF的度数．