题目内容
 如图,△ABC的角平分线BD、CE相交于点P.
如图,△ABC的角平分线BD、CE相交于点P.(1)已知∠ABC=50°,∠ACB=60°,求∠BPC的度数;
(2)若∠ABC+∠ACB=110°,求∠BPC的度数;
(3)若∠A=70°,求∠BPC的度数.变式∠A=n°,求∠BPC的度数.思考,你能找出∠A和∠BPC的大小关系吗?
考点:三角形内角和定理
专题:
分析:先根据角平分线的定义得到∠1=
∠ABC,∠2=
∠ACB,再根据三角形内角和定理得∠BPC=180°-∠1-∠2=180°-
(∠ABC+∠ACB),加上∠ABC+∠ACB=180°-∠A,易得∠BPC=90°+
∠A,然后根据此结论解决各小题.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵∠ABC,∠ACB的平分线相交于点P,
∴∠1=
∠ABC,∠2=
∠ACB,
∴∠BPC=180°-∠1-∠2=180°-
∠ABC-
∠ACB=180°-
(∠ABC+∠ACB),
∵∠ABC+∠ACB=180°-∠A,
∴∠BPC=180°-
(180°-∠A)=90°+
∠A,
(1)∵∠ABC=50°,∠ACB=60°,
∴∠A=180°-50°-60°=70°,
∴∠BPC=90°+
×70°=125°;
(2)∵∠ABC+∠ACB=110°,
∴∠A=180°-110°=70°,
∴∠BPC=90°+
×70°=125°;
(3)∵∠A=70°,
∴∠BPC=90°+
×70°=125°;
当∠A=n°,∠BPC=90°+
n;
∠BOC与∠A的数量关系为∠BPC=90°+
∠A.
∴∠1=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BPC=180°-∠1-∠2=180°-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵∠ABC+∠ACB=180°-∠A,
∴∠BPC=180°-
| 1 |
| 2 |
| 1 |
| 2 |
(1)∵∠ABC=50°,∠ACB=60°,
∴∠A=180°-50°-60°=70°,
∴∠BPC=90°+
| 1 |
| 2 |
(2)∵∠ABC+∠ACB=110°,
∴∠A=180°-110°=70°,
∴∠BPC=90°+
| 1 |
| 2 |
(3)∵∠A=70°,
∴∠BPC=90°+
| 1 |
| 2 |
当∠A=n°,∠BPC=90°+
| 1 |
| 2 |
∠BOC与∠A的数量关系为∠BPC=90°+
| 1 |
| 2 |
点评:本题考查了三角形内角和定理:三角形内角和是180°.本题探讨了三角形两角的平分线的夹角与第三个角之间的关系.

练习册系列答案
相关题目
 如图,已知四边形ABCD内接于⊙O,直径AC=6,对角线AC、BD交于E点,且AB=BD,EC=1,则AD的长为( )
如图,已知四边形ABCD内接于⊙O,直径AC=6,对角线AC、BD交于E点,且AB=BD,EC=1,则AD的长为( )A、
| ||||
B、
| ||||
C、
| ||||
D、3
|
一个彩条链条,有红、黄、绿三种颜色的钢环按顺序重复排列,其中省略了一部分(如图所示),则这根彩色链条共有钢环的个数可能是( )


| A、2012 | B、2013 |
| C、2014 | D、2015 |
 如图,在第1个△A1BC中,∠B=30°,A1B=CB;在边A1B上任取一点D,延长CA1到A2,使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3,使A2A3=A2E,得到第3个△A2A3E,…按此做法继续下去,则第n个三角形中以An为顶点的内角度数是
如图,在第1个△A1BC中,∠B=30°,A1B=CB;在边A1B上任取一点D,延长CA1到A2,使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3,使A2A3=A2E,得到第3个△A2A3E,…按此做法继续下去,则第n个三角形中以An为顶点的内角度数是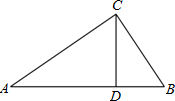 如图,Rt△ABC中,∠ACB=90°,CD是AB边上的高,AC=16,BC=12,求CD的长.
如图,Rt△ABC中,∠ACB=90°,CD是AB边上的高,AC=16,BC=12,求CD的长.
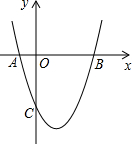 如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点.
如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点.