题目内容
2.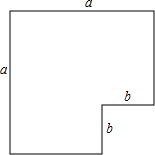 如图是由边长为a的正方形剪去一个边长为b的小正方形后余下的图形.把图剪开后,再拼成一个四边形,可以用来验证公式:a2-b2=(a+b)(a-b).
如图是由边长为a的正方形剪去一个边长为b的小正方形后余下的图形.把图剪开后,再拼成一个四边形,可以用来验证公式:a2-b2=(a+b)(a-b).(1)请你通过对图的剪拼,画出三种不同拼法的示意图.要求:
①拼成的图形是四边形;
②在图上画剪切线(用虚线表示);
③在拼出的图形上标出已知的边长.
(2)感受平方差公式的无字证明,并用公式巧算下题;
①2(3+1)(32+1)(34+1)…(332+1)+1
②1002-992+982-972+962-952+…22-12.
分析 (1)①将原图片剪成两部分,它们分别是边长为a、a-b和b、a-b的矩形,可拼成一个边长为a-b、a+b的矩形;
②沿对角线将原图分成两个直角梯形,将它们的高重合,拼成一个等腰梯形;
③将原图沿小正方形的边剪开,分成三个小矩形,然后三个小矩形又可拼成一个大矩形.
(2)①将2拆成3-1,然后依次与后一项按照平方差公式计算可得;
②将每两个相邻整数的平方差按照公式展开,化为连续整数相加,计算可得结果.
解答 解:(1)
①、
②、
③、
(2)①2(3+1)(32+1)(34+1)…(332+1)+1
=(3-1)(3+1)(32+1)(34+1)…(332+1)+1
=(32-1)(32+1)(34+1)…(332+1)+1
=(34-1)(34+1)…(332+1)+1
…
=364-1+1
=364;
②1002-992+982-972+962-952+…22-12
=(100+99)(100-99)+(98+97)(98-97)+(96+95)(96-95)+…+(2+1)(2-1)
=100+99+98+97+…+2+1
=$\frac{100×(100+1)}{2}$
=5050.
点评 本题考查了平方差公式几何意义的理解,将整式运算与几何图形结合,注意各个量的变化.

练习册系列答案
相关题目
12.下列等式中,从等号左边到右边的变形是因式分解的是( )
| A. | x2-9+8x=(x-3)(x+3)+8x | B. | -5x2y3=-5xy•(xy2) | ||
| C. | x2-4x-5=x(x-4-$\frac{5}{x}$) | D. | -x2+2xy=-x(x-2y) |
10.上网费包括网络使用费(每月38元)和上网通讯费(每小时2元),某电信局对拨号上网用户实行优惠,具体优惠政策如下:
(1)若小明家四月份上网28小时,应缴上网费多少?
(2)若小明家五月份上网80小时,应缴上网费多少元?
(3)如果用x表示每月的上网时间,y表示上网费用,你能用代数式分别表示出各时间段的上网费用吗?
| 上网时间 | 优惠标准 |
| 0~30小时(不超过30) | 无优惠 |
| 30~50小时(不超过50) | 通讯费优惠30% |
| 50~100小时(不超过100) | 通讯费优惠40% |
| 100小时以上 | 通讯费优惠50% |
(2)若小明家五月份上网80小时,应缴上网费多少元?
(3)如果用x表示每月的上网时间,y表示上网费用,你能用代数式分别表示出各时间段的上网费用吗?
11.有下列四个命题,其中正确的是( )
| A. | 平分弦的直径垂直于弦 | |
| B. | 三点确定一个圆 | |
| C. | 三角形的内心到三角形三个顶点的距离相等 | |
| D. | 相等的弧所对的圆心角相等 |
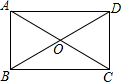 如图,矩形ABCD的对角线AC、BD相交于点O,AB=3,∠COD=60°,则AD的长为3$\sqrt{3}$.
如图,矩形ABCD的对角线AC、BD相交于点O,AB=3,∠COD=60°,则AD的长为3$\sqrt{3}$. 如图,△ABC为等腰三角形,AB=AC,BD为△ABC的高,E点在AB上,G点在BC上,且满足∠DEG=45°,∠DBC=∠BEG.若$\frac{FG}{BC}$=$\frac{1}{5}$,则$\frac{AE}{BE}$的值为$\frac{1}{4}$.
如图,△ABC为等腰三角形,AB=AC,BD为△ABC的高,E点在AB上,G点在BC上,且满足∠DEG=45°,∠DBC=∠BEG.若$\frac{FG}{BC}$=$\frac{1}{5}$,则$\frac{AE}{BE}$的值为$\frac{1}{4}$.