题目内容
17.如图1,等腰△ABC中,AB=AC,经过点C的直线l与边AB平行,点P是线段BC上一点,连接AP,作∠APE=∠BAC,角的一边PE交直线l于点E.(1)探究线段PA与PE的数量关系,并加以说明;
(2)若将图1中“点P是线段BC上一点”改为“点P是射线BC上一点”,其他条件不变,(1)的结论是否成立?如果成立,请给予证明;如果不成立,请说明理由.

分析 (1)连接AE,由平行线的性质得出∠BAC=∠ACE,∠2=∠B,再由已知条件得出∠APE=∠ACE,证出A、P、C、E四点共圆,由圆周角定理得出∠1=∠3,∠2=∠PAE,由等腰三角形的性质得出∠B=∠3,得出∠2=∠3,证出∠PAE=∠1,即可得出结论;
(2)连接AE由平行线的性质得出∠BAC=∠ACE,∠2=∠B,再由已知条件得出∠APE=∠ACE,证出A、C、P、E四点共圆,由圆周角定理得出∠1=∠2,∠3=∠PEA,由等腰三角形的性质得出∠B=∠3,得出∠2=∠3,证出∠PEA=∠1,即可得出结论.
解答 (1)解:PA=PE,理由如下:连接AE,如图1所示: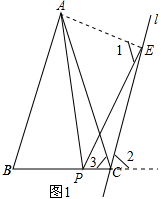
∵AB∥CE,
∴∠BAC=∠ACE,∠2=∠B,
∵∠APE=∠BAC,
∴∠APE=∠ACE,
∴A、P、C、E四点共圆,
∴∠1=∠3,∠2=∠PAE,
∵AB=AC,
∴∠B=∠3,
∴∠2=∠3,
∴∠PAE=∠1,
∴PA=PE;
(2)解:若将图1中“点P是线段BC上一点”改为“点P是射线BC上一点”,其他条件不变,(1)的结论成立;理由如下:
连接AE,如图2所示: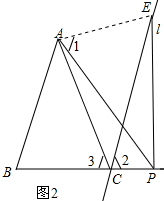
∵AB∥CE,
∴∠BAC=∠ACE,∠2=∠B,
∵∠APE=∠BAC,
∴∠APE=∠ACE,
∴A、C、P、E四点共圆,
∴∠1=∠2,∠3=∠PEA,
∵AB=AC,
∴∠B=∠3,
∴∠2=∠3,
∴∠PEA=∠1,
∴PA=PE.
点评 本题考查了四点共圆、圆周角定理、等腰三角形的性质与判定、圆内接四边形的性质、平行线的性质等知识;本题综合性强,有一定难度.

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目