题目内容
8．
如图，AB⊥BD于点B，AC⊥CD于点C，且AC与BD相交于点E，则△ADE的边DE上高是AB；边AE上的高为CD；若AE=5，ED=2，CD=$\frac{9}{5}$，则AB=$\frac{9}{2}$．
分析 根据三角形高的定义即可判断，利用S△ADE=$\frac{1}{2}$•DE•AB=$\frac{1}{2}$•AE•CD，即可求出AB．
解答 解：如图，∵AB⊥BD于点B，AC⊥CD于点C，
∴△ADE的边DE上高是 AB；边AE上的高为CD，
∴S△ADE=$\frac{1}{2}$•DE•AB=$\frac{1}{2}$•AE•CD，
∴AB=$\frac{AE•CD}{DE}$=$\frac{5×\frac{9}{5}}{2}$=$\frac{9}{2}$，
故答案为AB，CD，$\frac{9}{2}$．
点评 本题考查三角形的高的定义、三角形的面积等知识，掌握基本概念是解题的关键是，学会用面积法求线段的长．
练习册系列答案
相关题目
如图，正方形ABCD的边长为4，点B的坐标为（3，1），AB∥x轴，AD∥y轴，则点D的坐标为（-1，5）．
如图，四边形ABCD中，AD∥BC，∠C=132°，过点A作AE⊥BC，连接DE，若DE平分∠ADC，求∠AED的度数．
已知实数a，b在数轴上的位置如图所示，且|a|＞|b|，化简$\sqrt{（a+b）^{2}}$-|a-b|．
一副三角板按如图方式摆放，得到△ABD和△BCD，其中∠ADB=∠BCD=90°，∠A=60°，∠CBD=45°，E为AB的中点，过点E作EF⊥CD于点F．若AD=4cm，则EF的长为（$\sqrt{2}$+$\sqrt{6}$）cm．
如图，在直角坐标平面内，△ABC的顶点A（-1，0），点B与点A关于原点对称，AB=BC，∠CAB=30°，将△ABC绕点C旋转，使点A落在x轴上的点D处，点B落在点E处，那么BE所在直线的解析式为y=$\frac{\sqrt{3}}{3}$x-$\frac{\sqrt{3}}{3}$．
20．
如图，已知四边形ABCD是平行四边形，下列结论中错误的是（ ）
如图，已知四边形ABCD是平行四边形，下列结论中错误的是（ ）| A． | 当AB=BC时，它是菱形 | B． | 当AC⊥BD时，它是菱形 | ||
| C． | 当AC=BD时，它是矩形 | D． | 当∠ABC=90°时，它是正方形 |
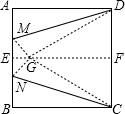我们知道，三边都相等的三角形是等边三角形，等边三角形的每一个内角都是60°，如图，先将正方形ABCD对折，折痕为EF，将这个正方形展平后，再分别将A、B对折，使点A、点B都与折痕EF上的点G重合，则∠NCG的度数是15度．
18．下列图形中，是中心对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |