题目内容
13.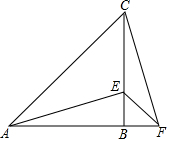 已知:如图,在△ABC中,AB=AC,∠ABC=90°,F为AB延长线上一点,点E在BC上,BE=CF,连接AE、EF和CF.
已知:如图,在△ABC中,AB=AC,∠ABC=90°,F为AB延长线上一点,点E在BC上,BE=CF,连接AE、EF和CF.(1)求证:AE=CF;
(2)若∠CAE=20°,求∠EFC的度数.
分析 (1)欲证明AE=CF,只要证明△ABE≌△CBF( SAS)即可.
(2)根据∠AEB=∠BFC,求出∠BFC,根据∠EFC=∠BFC-∠EFB即可解决问题.
解答 (1)证明:在△ABE和△CBF中,
$\left\{\begin{array}{l}AB=AB\\∠ABE=∠CBF\\ BE=BF\end{array}\right.$,
∴△ABE≌△CBF( SAS)
∴AE=CF
(2)解:∵∠ABC=90°,AB=BC,
∴∠CAB=45°,
∵∠CAE=20°,
∴∠EAB=45°-20°=25°,
∴∠BCF=∠EAB=25°,
∵∠CBF=90°,
∴∠BFC=180°-25°-90°=65°,
∵∠EBF=90°,BE=BF,
∴∠EFB=45°,
∴∠EFC=∠BFC-∠EFB=20°.
点评 本题考查全等三角形的判定和性质、等腰直角三角形的性质等知识,解题的关键是正确寻找全等三角形,利用全等三角形的性质解决问题,属于中考常考题型.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 如图,∠B与∠BCD互为余角,∠B=∠ACD,DE⊥BC,垂足为E,AC与DE平行吗?
如图,∠B与∠BCD互为余角,∠B=∠ACD,DE⊥BC,垂足为E,AC与DE平行吗?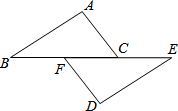 已知:点B、F、C、E在同一条直线上,FB=CE,AC=DF,现给出下列条件:①AB=ED;②∠A=∠D=90°;③∠ACB=∠DFE.请你从上面三个条件中选择一个合适的条件,添加到已知条件中,使得AB∥ED成立,并给出证明.
已知:点B、F、C、E在同一条直线上,FB=CE,AC=DF,现给出下列条件:①AB=ED;②∠A=∠D=90°;③∠ACB=∠DFE.请你从上面三个条件中选择一个合适的条件,添加到已知条件中,使得AB∥ED成立,并给出证明.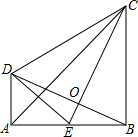 如图,CB⊥AB,垂足为B,DA⊥AB,垂足为A,E为AB的中点,AB=BC,CE⊥BD.
如图,CB⊥AB,垂足为B,DA⊥AB,垂足为A,E为AB的中点,AB=BC,CE⊥BD.