题目内容
3.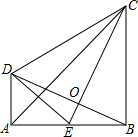 如图,CB⊥AB,垂足为B,DA⊥AB,垂足为A,E为AB的中点,AB=BC,CE⊥BD.
如图,CB⊥AB,垂足为B,DA⊥AB,垂足为A,E为AB的中点,AB=BC,CE⊥BD.(1)BE与AD是否相等?为什么?
(2)求证:AC是线段DE的垂直平分线;
(3)∠DBC与∠DCB相等吗?试说明理由.
分析 (1)由BC⊥AB,DA⊥AB,CE⊥BD,得到∠ADB=∠EBC=∠COB=90°,根据余角的性质得到∠ABD=∠BCE,证得△ABD≌△BCE,根据全等三角形的性质即可得到结论;
(2)由线段垂直平分线的性质结论;
(3)根据等腰三角形的性质即可得到结论.
解答 解:(1)AD=BE,
理由:∵BC⊥AB,DA⊥AB,CE⊥BD,
∠ADB=∠EBC=∠COB=90°,
∴∠ABD+∠CBD=∠OCB+∠ABD=90°,
∴∠ABD=∠BCE,
在△ABD与△BCE中,$\left\{\begin{array}{l}{∠DAB=∠EBC}\\{AB=BC}\\{∠ABD=∠BCE}\end{array}\right.$,
∴△ABD≌△BCE,
∴AD=BE,
(2)∵AE=BE,∴AD=AE,
∵DA⊥AB,
∴∠EAD=90°,
∴∠CAB=∠DAC=45°,
∴AC垂直平分DE,
(3)∠DBC=∠DCB,
理由:∵AC垂直平分DE,
∴CD=CE,
∵CE=BD,
∴CD=BD,
∴∠DBC=∠DCB.
点评 本题考查了全等三角形的判定与性质,线段垂直平分线的性质,等腰直角三角形的性质,等式的性质,特别注意等量之间的代换.

练习册系列答案
相关题目
13.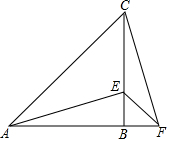 已知:如图,在△ABC中,AB=AC,∠ABC=90°,F为AB延长线上一点,点E在BC上,BE=CF,连接AE、EF和CF.
已知:如图,在△ABC中,AB=AC,∠ABC=90°,F为AB延长线上一点,点E在BC上,BE=CF,连接AE、EF和CF.
(1)求证:AE=CF;
(2)若∠CAE=20°,求∠EFC的度数.
 已知:如图,在△ABC中,AB=AC,∠ABC=90°,F为AB延长线上一点,点E在BC上,BE=CF,连接AE、EF和CF.
已知:如图,在△ABC中,AB=AC,∠ABC=90°,F为AB延长线上一点,点E在BC上,BE=CF,连接AE、EF和CF.(1)求证:AE=CF;
(2)若∠CAE=20°,求∠EFC的度数.
13.∠α与∠β的度数分别是 2m-67和 68-m,且∠α与∠β都是∠γ 的补角,那么∠α与∠β的关系是( )
| A. | 互余但不相等 | B. | 互为补角 | C. | 相等但不互余 | D. | 互余且相等 |
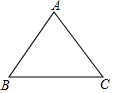 已知在三角形ABC中,AB=AC=5,BC=6,求三角形ABC的面积.
已知在三角形ABC中,AB=AC=5,BC=6,求三角形ABC的面积.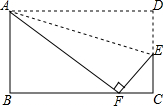 如图,小红将长方形ABCD沿AE折叠,顶点D恰好落在BC边上的F处,已知AB=8,BC=10,试求折痕AE的长.
如图,小红将长方形ABCD沿AE折叠,顶点D恰好落在BC边上的F处,已知AB=8,BC=10,试求折痕AE的长.