题目内容
19.△ABC的三边分别为a,b,c,满足下列条件的△ABC不是直角三角形的是( )| A. | c2-a2=b2 | B. | ∠A-∠C=∠B | C. | a:b:c=20:21:29 | D. | ∠A:∠B:∠C=2:3:4 |
分析 根据勾股定理的逆定理判断A、C即可;根据三角形内角和定理判断B、D即可.
解答 解:A、∵c2-a2=b2,
∴c2=b2+a2,
∴△ABC是直角三角形,故本选项不符合题意;
B、∵∠A-∠C=∠B,
∴∠B+∠C=∠A,
∵∠A+∠B+∠C=180°,
∴2∠A=180°,
∴∠A=90°,即△ABC是直角三角形,故本选项不符合题意;
C、∵202+212=292,
∴△ABC是直角三角形,故本选项不符合题意;
D、∵∠A:∠B:∠C=2:3:4,∠A+∠B+∠C=180°,
∴∠A=40°,∠B=60°,∠C=80°,
∴△ABC不是直角三角形,故本选项符合题意;
故选D.
点评 本题考查了三角形内角和定理,勾股定理的逆定理的应用,主要考查学生的计算能力和辨析能力.

练习册系列答案
相关题目
9.下列计算结果为负值的是( )
| A. | (-3)÷(-2) | B. | 0×(-7) | C. | 1-9 | D. | -7-(-10) |
10.若A(-1,y1),B(1,y2),C(2,y3)是y=$\frac{2}{x}$上的三个点,则y1,y2,y3之间的大小关系正确的是( )
| A. | y1>y2>y3 | B. | y1<y2<y3 | C. | y3>y1>y2 | D. | y1<y3<y2 |
7.下列哪种统计图(表)最不适合用来表示某校男、女学生的人数( )
| A. | 扇形统计图 | B. | 条形统计图 | C. | 折线统计图 | D. | 数据统计表 |
14.4.9×105是一个由四舍五入得到的近似数,它是( )
| A. | 精确到百分位 | B. | 精确到十分位 | C. | 精确到万位 | D. | 精确到十万位 |
4.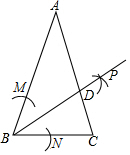 △ABC中,AB=AC,∠ABC=72°,以B为圆心,以任意长为半径画弧,分别交BA、BC于M、N,再分别以M、N为圆心,以大于$\frac{1}{2}$MN为半径画弧,两弧交于点P,射线BP交AC于点D,则图中与BC相等的线段有( )
△ABC中,AB=AC,∠ABC=72°,以B为圆心,以任意长为半径画弧,分别交BA、BC于M、N,再分别以M、N为圆心,以大于$\frac{1}{2}$MN为半径画弧,两弧交于点P,射线BP交AC于点D,则图中与BC相等的线段有( )
 △ABC中,AB=AC,∠ABC=72°,以B为圆心,以任意长为半径画弧,分别交BA、BC于M、N,再分别以M、N为圆心,以大于$\frac{1}{2}$MN为半径画弧,两弧交于点P,射线BP交AC于点D,则图中与BC相等的线段有( )
△ABC中,AB=AC,∠ABC=72°,以B为圆心,以任意长为半径画弧,分别交BA、BC于M、N,再分别以M、N为圆心,以大于$\frac{1}{2}$MN为半径画弧,两弧交于点P,射线BP交AC于点D,则图中与BC相等的线段有( )| A. | BD | B. | CD | C. | BD和AD | D. | CD和AD |
11.一元二次方程x2+2x-1=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 只有一个实数根 | D. | 没有实数根 |
8. 如图所示,AD平分∠BAC,AB=AC,连结BD、CD并延长分别交AC、AB于F、E点,则此图中全等三角形的对数为( )
如图所示,AD平分∠BAC,AB=AC,连结BD、CD并延长分别交AC、AB于F、E点,则此图中全等三角形的对数为( )
 如图所示,AD平分∠BAC,AB=AC,连结BD、CD并延长分别交AC、AB于F、E点,则此图中全等三角形的对数为( )
如图所示,AD平分∠BAC,AB=AC,连结BD、CD并延长分别交AC、AB于F、E点,则此图中全等三角形的对数为( )| A. | 2对 | B. | 3对 | C. | 4对 | D. | 5对 |