��Ŀ����
��1����ͼ������ABCD�У�AB=5cm��BC=2cm����AB����ȡһ��E������E��A��B���غϣ�������CE��DE���־���ABCD���ɵ�3�������ζ����ƣ����ǰ������ĵ�E��������ABCD��AB���ϵ�ȫ���Ƶ㣬��ͼ��AB���ϻ�������Ҫ���ȫ���Ƶ�E������AE�ij�������ͼ���߲��ޣ����Լ�˵����
��2����������һ������ABCD��AB�����Ƿ�һ������������ȫ���Ƶ�E�����һ�����ڣ���˵�����ɣ������һ�����ڣ������˵����
��3�����ı���ABCD�У�AD��BC��AD��BC����B=90�㣬����E���ı���ABCD��AB���ϵ�һ��ȫ���Ƶ�ʱ����̽����AE��BE��������ϵ����˵�����ɣ�

��2����������һ������ABCD��AB�����Ƿ�һ������������ȫ���Ƶ�E�����һ�����ڣ���˵�����ɣ������һ�����ڣ������˵����
��3�����ı���ABCD�У�AD��BC��AD��BC����B=90�㣬����E���ı���ABCD��AB���ϵ�һ��ȫ���Ƶ�ʱ����̽����AE��BE��������ϵ����˵�����ɣ�
��������1���������������ζ�Ӧ����ȿɵá�A=��B=��CED������CDΪֱ����Բ����AB�Ľ��㼴Ϊ����ĵ�E���������������ζ�Ӧ�߳ɱ�����ʽ��⼴�ɵõ�AE��ֵ��
��2�����ݣ�1���������������εĿ����ڳ���һ�룬��Բ����һ��û�н��㣬Ҳ�Ͳ�����ȫ���Ƶ㣻
��3������ȫ���Ƶ�Ķ���ɵá�ADE�͡�BEC���ƣ��ٸ������������ζ�Ӧ�߳ɱ�����ʽ��⼴�ɣ�
��2�����ݣ�1���������������εĿ����ڳ���һ�룬��Բ����һ��û�н��㣬Ҳ�Ͳ�����ȫ���Ƶ㣻
��3������ȫ���Ƶ�Ķ���ɵá�ADE�͡�BEC���ƣ��ٸ������������ζ�Ӧ�߳ɱ�����ʽ��⼴�ɣ�
��� �⣺��1����ͼ���ھ���ABCD�У���A=��B=90�㣬
�⣺��1����ͼ���ھ���ABCD�У���A=��B=90�㣬
�����������ζ����ƣ�
���CED=90�㣬
��CDΪֱ������O����AB�ཻ�����㼴Ϊ��E��
��AE=x����BE=AB-AE=5-x��
�ߡ�ADE�ס�BEC��
��
=
��
��
=
��
�����ã�x1=1��x2=4��
���ԣ�AE�ij�Ϊ1cm��4cm��
��2���ɣ�1����֪�������εij�AB��2ADʱ��Բ��ABû�н��㣬����AB���ϲ�����������ȫ���Ƶ�E��
��3��AE��BE��������ϵΪ��AE•BE=AD•BC��
�������£���ͼ���ߵ�E���ı���ABCD��AB���ϵ�һ��ȫ���Ƶ㣬
���ADE�ס�BEC��
��
=
��
��AE•BE=AD•BC��
 �⣺��1����ͼ���ھ���ABCD�У���A=��B=90�㣬
�⣺��1����ͼ���ھ���ABCD�У���A=��B=90�㣬�����������ζ����ƣ�
���CED=90�㣬
��CDΪֱ������O����AB�ཻ�����㼴Ϊ��E��
��AE=x����BE=AB-AE=5-x��
�ߡ�ADE�ס�BEC��
��
| AE |
| BC |
| AD |
| BE |
��
| x |
| 2 |
| 2 |
| 5-x |

�����ã�x1=1��x2=4��
���ԣ�AE�ij�Ϊ1cm��4cm��
��2���ɣ�1����֪�������εij�AB��2ADʱ��Բ��ABû�н��㣬����AB���ϲ�����������ȫ���Ƶ�E��
��3��AE��BE��������ϵΪ��AE•BE=AD•BC��
�������£���ͼ���ߵ�E���ı���ABCD��AB���ϵ�һ��ȫ���Ƶ㣬
���ADE�ס�BEC��
��
| AD |
| BE |
| AE |
| BC |
��AE•BE=AD•BC��
�����������������������ۺ��⣬��Ҫ���������������εĶ�Ӧ�߳ɱ��������ʣ�������Ŀ��Ϣ������ȫ���Ƶ�Ķ��壬�жϳ���CED=90�㣬�Ӷ�ȷ������CDΪֱ����Բ�ǽ���Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
 ��ͼ������ABCD�У�BC=2��DC=4����ABΪֱ���İ�ԲO��DC�����ڵ�E������Ӱ���ֵ����Ϊ
��ͼ������ABCD�У�BC=2��DC=4����ABΪֱ���İ�ԲO��DC�����ڵ�E������Ӱ���ֵ����Ϊ ��ͼ������ABCD���ܳ�Ϊ12cm��EΪBC���е㣬AE��ED�ڵ�E����AB=
��ͼ������ABCD���ܳ�Ϊ12cm��EΪBC���е㣬AE��ED�ڵ�E����AB=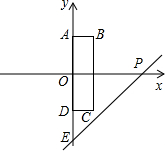 ��ͼ������ABCD�ı�AD��y���ϣ�AD���е���ԭ��O�غϣ�AB=1��AD=2��������P��3��0����y���ϵĶ���E��0��b����ֱ�������ABCD�ı��й����㣬��b��ȡֵ��Χ��
��ͼ������ABCD�ı�AD��y���ϣ�AD���е���ԭ��O�غϣ�AB=1��AD=2��������P��3��0����y���ϵĶ���E��0��b����ֱ�������ABCD�ı��й����㣬��b��ȡֵ��Χ��
 ��ͼ������ֽƬABCD�У�AB=4cm��BC=8cm���ֽ�ֽƬ�۵�ѹƽ��ʹA��C�غϣ����ۺ�ΪEF�����ص����֡�AEF���������
��ͼ������ֽƬABCD�У�AB=4cm��BC=8cm���ֽ�ֽƬ�۵�ѹƽ��ʹA��C�غϣ����ۺ�ΪEF�����ص����֡�AEF���������