题目内容
17.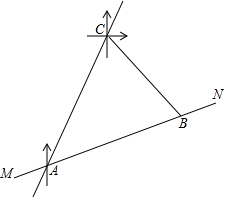 超速行驶是一种十分危险的违法驾驶行为,在一条笔直的高速公路MN上,小型车限速为每小时120千米,设置在公路旁的超速监测点C,现测得一辆小型车在监测点C的南偏西30°方向的A处,7秒后,测得其在监测点C的南偏东45°方向的B处,已知BC=200米,B在A的北偏东75°方向,请问:这辆车超速了吗?通过计算说明理由.(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
超速行驶是一种十分危险的违法驾驶行为,在一条笔直的高速公路MN上,小型车限速为每小时120千米,设置在公路旁的超速监测点C,现测得一辆小型车在监测点C的南偏西30°方向的A处,7秒后,测得其在监测点C的南偏东45°方向的B处,已知BC=200米,B在A的北偏东75°方向,请问:这辆车超速了吗?通过计算说明理由.(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
分析 直接构造直角三角形,再利用特殊角的三角函数关系得出AB的长,进而求出汽车的速度,进而得出答案.
解答 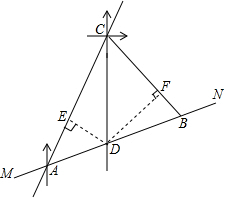 解:这辆汽车超速了,
解:这辆汽车超速了,
理由:过点D作DF⊥CB于点F,过点D作DE⊥AC于点E,
由题意可得:∠ACD=30°,∠DCB=45°,∠CDB=75°,则∠DAE=45°,∠CDF=45°,∠FDB=30°,
设BF=x,则DF=CF=$\sqrt{3}$x,
∵BC=200m,
∴$\sqrt{3}$x+x=200,
解得:x=100($\sqrt{3}$-1),
故BF=100($\sqrt{3}$-1)m,
则BD=200($\sqrt{3}$-1)m,
DC=$\sqrt{2}$DF=$\sqrt{2}$×$\sqrt{3}$×100($\sqrt{3}$-1)=(300$\sqrt{2}$-100$\sqrt{6}$)m,
故DE=(150$\sqrt{2}$-50$\sqrt{6}$)m,
则AD=$\sqrt{2}$(150$\sqrt{2}$-50$\sqrt{6}$)=(300-100$\sqrt{3}$)m,
故AB=AD+BD=300-100$\sqrt{3}$+200($\sqrt{3}$-1)=100($\sqrt{3}$+1)≈273(m),
∴$\frac{273}{7}$≈39(m/s),
∵每小时120千米=$\frac{100}{3}$≈33.3(m/s),
∵39>33.3,
∴这辆车已经超速.
点评 此题主要考查了解直角三角形的应用,正确构造直角三角形是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

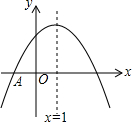 如图,抛物线y=ax2+bx+c与x轴交于点A(-1,0),顶点坐标(1,n),与y轴的交点在(0,3),(0,4)之间(包含端点),则下列结论:①abc>0;②3a+b<0;③-$\frac{4}{3}$≤a≤-1;④a+b≥am2+bm(m为任意实数);⑤一元二次方程ax2+bx+c=n有两个不相等的实数根,其中正确的有( )
如图,抛物线y=ax2+bx+c与x轴交于点A(-1,0),顶点坐标(1,n),与y轴的交点在(0,3),(0,4)之间(包含端点),则下列结论:①abc>0;②3a+b<0;③-$\frac{4}{3}$≤a≤-1;④a+b≥am2+bm(m为任意实数);⑤一元二次方程ax2+bx+c=n有两个不相等的实数根,其中正确的有( )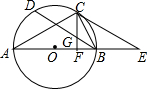 如图所示,以△ABC的边AB为直径作⊙O,点C在⊙O上,BD是⊙O的弦,∠A=∠CBD,过点C作CF⊥AB于点F,交BD于点G,过C作CE∥BD交AB的延长线于点E.
如图所示,以△ABC的边AB为直径作⊙O,点C在⊙O上,BD是⊙O的弦,∠A=∠CBD,过点C作CF⊥AB于点F,交BD于点G,过C作CE∥BD交AB的延长线于点E.