题目内容
 如图,在直角梯形ABCD中,AB=BC=6,点E为BC边上一点,且∠EAD=45°,ED=5,则△ADE的面积为
如图,在直角梯形ABCD中,AB=BC=6,点E为BC边上一点,且∠EAD=45°,ED=5,则△ADE的面积为考点:全等三角形的判定与性质,正方形的判定与性质,直角梯形
专题:
分析:过A作AF⊥CD于F,在四边形ABCF是正方形,延长CB到G,使BG=DF,先证得△AGB≌△ADF得出AG=AD,∠EAD=∠GAE=45°,然后再证得△ADE≌△AGE,得出EG=ED=5,最后根据全等三角形的面积相等即可求得;
解答: 解:过A作AF⊥CD于F,在四边形ABCF是正方形,延长CB到G,使BG=DF,
解:过A作AF⊥CD于F,在四边形ABCF是正方形,延长CB到G,使BG=DF,
在△AGB与△ADF中
∴△AGB≌△ADF(SAS),
∴AG=AD,∠GAB=∠DAF,
∴∠GAD=90°
∵∠EAD=45°,
∴∠GAE=45°,
在△ADE与△AGE中
∴△ADE≌△AGE(SAS),
∴EG=ED=5,
∴S△ADE=S△AGE=
EG•AB=
×5×6=15,
故答案为15.
 解:过A作AF⊥CD于F,在四边形ABCF是正方形,延长CB到G,使BG=DF,
解:过A作AF⊥CD于F,在四边形ABCF是正方形,延长CB到G,使BG=DF,在△AGB与△ADF中
|
∴△AGB≌△ADF(SAS),
∴AG=AD,∠GAB=∠DAF,
∴∠GAD=90°
∵∠EAD=45°,
∴∠GAE=45°,
在△ADE与△AGE中
|
∴△ADE≌△AGE(SAS),
∴EG=ED=5,
∴S△ADE=S△AGE=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为15.
点评:本题考查了三角形全等的判定和性质,正方形的性质,作出辅助线根据全等的三角形是本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
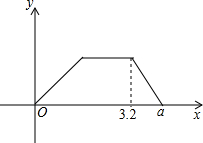 一辆货车从甲地匀速驶往乙地,到达后用了半小时卸货,随即匀速返回,已知货车返回的速度是它从甲地驶往乙地的速度的1.5倍.货车离甲地的距离y(千米)关于时间x(小时)的函数图象如图所示.则a=
一辆货车从甲地匀速驶往乙地,到达后用了半小时卸货,随即匀速返回,已知货车返回的速度是它从甲地驶往乙地的速度的1.5倍.货车离甲地的距离y(千米)关于时间x(小时)的函数图象如图所示.则a= 如图,七年级(下)教材第4页给出了利用三角尺和直尺画平行线的一种方法,能说明AB∥DE的条件是( )
如图,七年级(下)教材第4页给出了利用三角尺和直尺画平行线的一种方法,能说明AB∥DE的条件是( )| A、∠CAB=∠FDE |
| B、∠ACB=∠DFE |
| C、∠ABC=∠DEF |
| D、∠BCD=∠EFG |
 已知,如图,AC⊥BC,CD⊥AB于D,则图中有
已知,如图,AC⊥BC,CD⊥AB于D,则图中有 如图,已知正方形ABCD,顶点A、D在y轴上,A点的坐标为(0,-1),D点的坐标为(0,2).若反比例函数y=
如图,已知正方形ABCD,顶点A、D在y轴上,A点的坐标为(0,-1),D点的坐标为(0,2).若反比例函数y=