题目内容
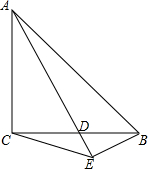如图，在等腰Rt△ABC中，∠C=90°，点D是BC上任意一点，连接AD，过点B作BE垂直于AD，交射线AD于点E，连接CE，求∠AEC的度数．考点：相似三角形的判定与性质,等腰直角三角形
专题：
分析：由题意可先证得△ACD∽△BED，所以有
=
，即有
=
，所以可证得△CDE∽△ADB，所以有∠AEC=∠ABD=45°．
| DE |
| CD |
| BD |
| AD |
| DE |
| BD |
| CD |
| AD |
解答：解：∵∠C=90°，BE⊥AD，
∴∠ACD=∠DEB，且∠ADC=∠BDE，
∴△ACD∽△BED，
∴
=
，即有
=
，
且∠CDE=∠ADB，
∴△CDE∽△ADB，
∴∠AEC=∠ABD，
∵等腰Rt△ABC中，∠C=90°，
∴∠AEC=∠ABD=45°．
∴∠ACD=∠DEB，且∠ADC=∠BDE，
∴△ACD∽△BED，
∴
| DE |
| CD |
| BD |
| AD |
| DE |
| BD |
| CD |
| AD |
且∠CDE=∠ADB，
∴△CDE∽△ADB，
∴∠AEC=∠ABD，
∵等腰Rt△ABC中，∠C=90°，
∴∠AEC=∠ABD=45°．
点评：本题主要考查相似三角形的判定和性质的运用，解题的关键是寻找△CDE和△ADB的条件．
练习册系列答案
相关题目
如图：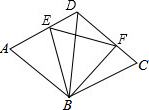
如图，△ABD和△BCD是等边三角形，∠EDF=60°，