题目内容
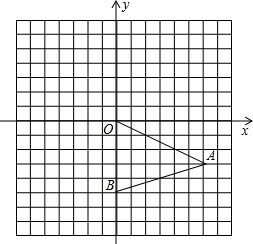 如图,在平面直角坐标系中,△OAB的三个顶点的坐标分别为A(6,-3),B(0,-5).
如图,在平面直角坐标系中,△OAB的三个顶点的坐标分别为A(6,-3),B(0,-5).(1)画出△OAB关于原点O的中心对称图形△OA1B1;
(2)画出△OAB绕原点O顺时针方向旋转90°后得到的△OA2B2;
(3)求△OAB旋转到△OA2B2时点A运动的路径长.
考点:作图-旋转变换,弧长的计算
专题:
分析:(1)分别作出点A、B关于原点O的对称的点,然后顺次连接;
(2)分别作出点A、B绕原点O顺时针方向旋转90°后的点,然后顺次连接;
(3)根据弧长公式求解即可.
(2)分别作出点A、B绕原点O顺时针方向旋转90°后的点,然后顺次连接;
(3)根据弧长公式求解即可.
解答:解:(1)所作图形如图所示:
(2)所作图形如图所示:
(3)OA=
=3
,
则点A运动的路径长L=
=
π.

(2)所作图形如图所示:
(3)OA=
| 32+62 |
| 5 |
则点A运动的路径长L=
90π×3
| ||
| 180 |
3
| ||
| 2 |
点评:本题考查了根据旋转变换作图以及弧长公式,解答本题的关键是根据网格结构找出对应点的位置.

练习册系列答案
相关题目
已知凸四边形ABCD中,∠A=∠C=90°.
(1)如图①,若DE平分∠ADC,BF平分∠ABC的邻补角,求证:DE⊥BF;
(2)如图②,若BF、DE分别平分∠ABC、∠ADC的邻补角,判断DE∥BF.

(1)如图①,若DE平分∠ADC,BF平分∠ABC的邻补角,求证:DE⊥BF;
(2)如图②,若BF、DE分别平分∠ABC、∠ADC的邻补角,判断DE∥BF.

若ab≠0,则
+
的值不可能是( )
| a |
| |a| |
| |b| |
| b |
| A、2 | B、0 | C、-2 | D、1 |
 如图,已知AD平分∠BAC,AB=AC,则此图中全等三角形有
如图,已知AD平分∠BAC,AB=AC,则此图中全等三角形有 已知:如图,D是AC上一点,BE∥AC,BE=AD,AE分别交BD、BC于点F、G,∠1=∠2.图中哪个三角形与△FAD全等?证明你的结论.
已知:如图,D是AC上一点,BE∥AC,BE=AD,AE分别交BD、BC于点F、G,∠1=∠2.图中哪个三角形与△FAD全等?证明你的结论.