题目内容
12.已知一个等腰三角形的两边长a、b满足方程组$\left\{\begin{array}{l}{4a-3b=11}\\{2a+b=13}\end{array}\right.$.(1)求a、b的值.
(2)求这个等腰三角形的周长.
分析 (1)根据加减消元法解二元一次方程组,即可求得a、b的值.
(2)讨论腰长的大小,再根据三角形三边关系即可得出答案.
解答 解:(1)$\left\{\begin{array}{l}{4a-3b=11①}\\{2a+b=13②}\end{array}\right.$,
②×2-①得5b=15,解得b=3,
把b=3代入②得2a+3=13,解得a=5;
(2)若a=5为腰长,5+5>3满足,此时三角形周长为:5×2+3=13;
若b=3为腰长,3+3>5满足,此时三角形周长为:3×2+5=11.
点评 本题考查了等腰三角形的性质及解二元一次方程组,难度一般,关键是掌握分类讨论的思想解题.

练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
17.下面是石林县某校八年级(1)班七位女同学的体重(单位:kg):51 50 40 43 48 48 63,这组数据的众数和中位数分别是( )
| A. | 48,43 | B. | 48,48 | C. | 43,48 | D. | 48,49 |
1.函数y=$\frac{\sqrt{x}}{1-x}$的自变量x的取值范围是( )
| A. | x≥0 | B. | x≠1 | C. | x>1 | D. | x≥0且x≠1 |
2.计算:$\sqrt{9x}$+2$\sqrt{\frac{x}{4}}$的结果是( )
| A. | 5x | B. | 3$\sqrt{x}$ | C. | 4$\sqrt{x}$ | D. | 4x2 |
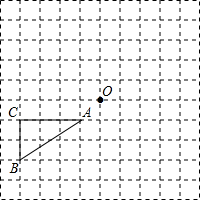 如图,在每个小正方形的边长均为1个单位长度的方格纸中,有△ABC.点A、B、C、O均在小正方形的顶点上.
如图,在每个小正方形的边长均为1个单位长度的方格纸中,有△ABC.点A、B、C、O均在小正方形的顶点上. 如图,直线AB,CD交于点O,OE⊥AB,若∠AOD=50°,则∠COE的度数为40°.
如图,直线AB,CD交于点O,OE⊥AB,若∠AOD=50°,则∠COE的度数为40°.