题目内容
2.△ABC三边中点分别为D、E、F,则S△ABC:S△DEF=( )| A. | 2 | B. | 3 | C. | 4 | D. | $\frac{1}{4}$ |
分析 由三角形中位线定理可知△ABC∽△DEF,且相似比为2:1,根据相似三角形的性质可求得答案.
解答  解:
解:
如图,
∵D、F为中点,
∴DF为△ABC的中位线,
∴DF∥BC,且BC=2DF,
同理可得AB=2EF,AC=2DE,
∴$\frac{AB}{EF}$=$\frac{AC}{DE}$=$\frac{BC}{DF}$=2,
∴△ABC∽△DEF,
∴$\frac{{S}_{△ABC}}{{S}_{△DEF}}$=($\frac{AB}{EF}$)2=4,
故选C.
点评 本题主要考查三角形中位线定理,由条件证明△ABC∽△DEF是解题的关键.

练习册系列答案
相关题目
10.若分式$\frac{{x}^{2}-25}{{x}^{2}-3x-10}$的值为0,则x的值是( )
| A. | ±5 | B. | 5 | C. | -5 | D. | 不存在 |
11. 如图,在△ABC中,∠ABC=∠C,DE垂直平分AB交AC于点D,若AB=6,BC=4,则△BCD的周长是( )
如图,在△ABC中,∠ABC=∠C,DE垂直平分AB交AC于点D,若AB=6,BC=4,则△BCD的周长是( )
 如图,在△ABC中,∠ABC=∠C,DE垂直平分AB交AC于点D,若AB=6,BC=4,则△BCD的周长是( )
如图,在△ABC中,∠ABC=∠C,DE垂直平分AB交AC于点D,若AB=6,BC=4,则△BCD的周长是( )| A. | 10 | B. | 12 | C. | 14 | D. | 16 |
12.二次函数y=(x+2)2+1的顶点坐标是( )
| A. | (2,1) | B. | (-2,1) | C. | (-2,-l) | D. | (2,-l) |
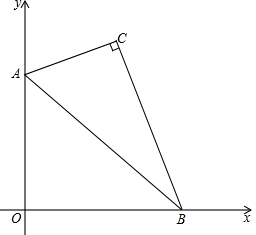 如图,将一块三内角分别为30°,60°,90°的三角板放置在直角坐标系中,三角板最长边的两个端点A、B分别在x轴、y轴的正半轴上滑动(不含坐标原点).已知:∠ACB=90°,∠CBA=30°,AB=12cm.
如图,将一块三内角分别为30°,60°,90°的三角板放置在直角坐标系中,三角板最长边的两个端点A、B分别在x轴、y轴的正半轴上滑动(不含坐标原点).已知:∠ACB=90°,∠CBA=30°,AB=12cm. 如图,已知∠1=60°,∠2=58°,∠3=60°,则∠4=122°.
如图,已知∠1=60°,∠2=58°,∠3=60°,则∠4=122°. 如图,平行四边形ABCD中,AB=8,AD=5,AE平分∠DAB交BC的延长线于F点,则CF=3.
如图,平行四边形ABCD中,AB=8,AD=5,AE平分∠DAB交BC的延长线于F点,则CF=3.