��Ŀ����
12��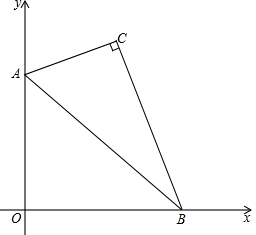 ��ͼ����һ�����ڽǷֱ�Ϊ30�㣬60�㣬90������ǰ������ֱ������ϵ�У����ǰ���ߵ������˵�A��B�ֱ���x�ᡢy����������ϻ�������������ԭ�㣩����֪����ACB=90�㣬��CBA=30�㣬AB=12cm��
��ͼ����һ�����ڽǷֱ�Ϊ30�㣬60�㣬90������ǰ������ֱ������ϵ�У����ǰ���ߵ������˵�A��B�ֱ���x�ᡢy����������ϻ�������������ԭ�㣩����֪����ACB=90�㣬��CBA=30�㣬AB=12cm����1��AC=6cm��
��2���ڵ�A��B�ֱ���x�ᡢy����������ϻ����Ĺ����У�����ACB�ա�AOBʱ����ֱ�Ƕ���C�����ꣻ
��3������B������ԭ����x�����ҷ����Ĺ����У�ֱ�Ƕ���CҲ��֮�˶���ֱ����A���ӽ�����ԭ�㣨������ԭ�㲻�غϣ�ʱ���˶�ֹͣ������C�˶���·�̳�Ϊl����l��ȡֵ��Χ��
���� ��1����ֱ�ǡ�ABC�У��������Ǻ������AC�ij���
��2���������Ǻ������BC�ij���Ȼ�����ȫ�������ε����ʣ����OB�ij�����CD��x���ڵ�D����ֱ�ǡ�BCD�У��������Ǻ������CD��BD����C�����꼴����ã�
��3��б��AB���е��·������OΪԲ�ģ���$\frac{1}{2}$ABΪ�뾶�Ļ���CҲ����������ڵ�Բ�ϣ���AB���е�·����ȣ����ݻ�����ʽ������⣮
��� �⣺��1����ֱ�ǡ�ABC�У�AC=AB•sin��CBA=12��$\frac{1}{2}$=6��cm����
�ʴ��ǣ�6��
��2����ֱ�ǡ�ABC�У�BC=AB•cos��CBA=12��$\frac{\sqrt{3}}{2}$=6$\sqrt{3}$��cm����
�١�ACB�ա�AOB��
��OB=BC=6$\sqrt{3}$����ABO=��CBA=30�㣬
���CBD=60�㣬
��CD��x���ڵ�D��
��ֱ�ǡ�BCD�У�BD=BC•cos��CBD=6$\sqrt{3}$��$\frac{1}{2}$=3$\sqrt{3}$��cm����
CD=BC•sin��CBD=6$\sqrt{3}$��$\frac{\sqrt{3}}{2}$=9��
��OD=OB-BD=6$\sqrt{3}$-3$\sqrt{3}$=3$\sqrt{3}$��
��C�������ǣ�3$\sqrt{3}$��9����
����ͼ��ʾ����ACB�ա�AOB��
BC=6$\sqrt{3}$��AC=6��
��C��6��6$\sqrt{3}$����
��3����Ϊ��RT��ABC�����Կ���AB�е㿴��Բ�ģ�A��B��C������ֱ���Բ�ϣ�C����˶�·�̼�AB�е���˶�·�̣�
AB���е��˶�·������OΪԲ�ģ���$\frac{1}{2}$AB=$\frac{1}{2}$��12=6��cm��Ϊ�뾶�Ļ�������Բ�Ľǽӽ�90�㣬
���ǣ�$\frac{90�С�6}{180}$=3�У�
��l�ķ�Χ�ǣ�0��l��3�У�
���� ������һ�κ��������Ǻ����Լ�ȫ�������ε����ʵ��ۺ��⣬��Ҫ������ͼ���۵������ʣ���ȷȷ��C���˶���·���ǹؼ���

 �Ƹ������������ϵ�д�
�Ƹ������������ϵ�д� һ���������κ��ĸ�ȫ�ȵ�С�����ΰ�ͼ�١������ַ�ʽ�ڷţ���ͼ�ڵĴ���������δ��С�����θ��Dz��ֵ�����ǣ��ú�a��b��ʽ�ӱ�ʾ����������
һ���������κ��ĸ�ȫ�ȵ�С�����ΰ�ͼ�١������ַ�ʽ�ڷţ���ͼ�ڵĴ���������δ��С�����θ��Dz��ֵ�����ǣ��ú�a��b��ʽ�ӱ�ʾ����������| A�� | ��a+b��2 | B�� | ��a-b��2 | C�� | 2ab | D�� | ab |
| A�� | 2 | B�� | 3 | C�� | 4 | D�� | $\frac{1}{4}$ |
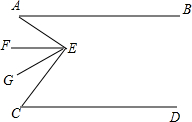 ��ͼ��AB��CD����A=30�㣬��C=60�㣬EF��EG���ȷ֡�AEC���ʣ�FE��GE���Ƿ������ABƽ�е�ֱ�ߣ�Ϊʲô����˵�����ɣ�
��ͼ��AB��CD����A=30�㣬��C=60�㣬EF��EG���ȷ֡�AEC���ʣ�FE��GE���Ƿ������ABƽ�е�ֱ�ߣ�Ϊʲô����˵�����ɣ� ��ͼ��ʾ��AD��BC�ڵ�D��EG��B�ڵ�G����E=��1����ADƽ�֡�BAC�����ж��Ƿ�EG��BC����˵�����ɣ�
��ͼ��ʾ��AD��BC�ڵ�D��EG��B�ڵ�G����E=��1����ADƽ�֡�BAC�����ж��Ƿ�EG��BC����˵�����ɣ�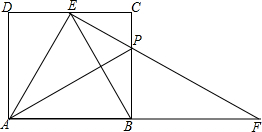 ��ͼ���ھ���ABCD�У�AB=2��AD=$\sqrt{3}$���ڱ�CD����һ��E��ʹEBƽ�֡�AEC����PΪBC����һ�㣬��BP=2CP������EP���ӳ���AB���ӳ�����F����������������ۣ�
��ͼ���ھ���ABCD�У�AB=2��AD=$\sqrt{3}$���ڱ�CD����һ��E��ʹEBƽ�֡�AEC����PΪBC����һ�㣬��BP=2CP������EP���ӳ���AB���ӳ�����F����������������ۣ�