题目内容
在对某二次三项式进行因式分解,小明同学看错了二次项系数而将分解为8(x-1)(2x-1),小敏同学因看错了一次项系数而将其分解为2(x-1)(9x-4),求这个多项式,并将此多项式进行正确的因式分解.
考点:因式分解的应用
专题:
分析:此题可以先将两个分解过的式子还原,再根据两个同学的错误得出正确的二次三项式,最后进行因式分解即可.
解答:
解:8(x-1)(2x-1)=16x2-24x+8,2(x-1)(9x-4)=18x2-26x+8;
由于小明同学因看错了二次项系数,小敏同学看错了一次项系数,
则正确的二次三项式为:18x2-24x+8;
再对其进行因式分解:18x2-24x+8=2(3x-2)2.
由于小明同学因看错了二次项系数,小敏同学看错了一次项系数,
则正确的二次三项式为:18x2-24x+8;
再对其进行因式分解:18x2-24x+8=2(3x-2)2.
点评:本题考查了因式分解的应用,理解题意,注意条件的结合运用.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
已知
+
=3,则代数式
的值为( )
| 1 |
| a |
| 1 |
| 2b |
| 2a-5ab+4b |
| 4ab-3a-6b |
| A、3 | ||
| B、-2 | ||
C、-
| ||
D、-
|
 如图,不能推出a∥b的条件是( )
如图,不能推出a∥b的条件是( )| A、∠1=∠3 |
| B、∠1=∠4 |
| C、∠2=∠4 |
| D、∠2+∠3=180° |
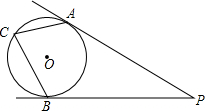 如图,PA、PB是⊙O的两条切线,切点分别是A、B,点C在⊙O上,若∠P=30°,则∠ACB=
如图,PA、PB是⊙O的两条切线,切点分别是A、B,点C在⊙O上,若∠P=30°,则∠ACB= 如图,已知E、A、B三点在同一直线上,AD是∠EAC的平分线,AD∥BC,∠B=50°,求∠EAD,∠C,∠BAC的度数.
如图,已知E、A、B三点在同一直线上,AD是∠EAC的平分线,AD∥BC,∠B=50°,求∠EAD,∠C,∠BAC的度数.