题目内容
 如图所示,在等腰三角形ABC中,∠A=90°,D是斜边BC的中点,
如图所示,在等腰三角形ABC中,∠A=90°,D是斜边BC的中点,(1)若E在直角边AB上运动,F在直角边AC上运动,在运动过程中始终保持BE=AF,试探求△EDF的形状,并说明理由.
(2)在(1)的条件下,四边形AEDF的面积是否发生变化?并证明你的结论.
考点:全等三角形的判定与性质,等腰直角三角形
专题:
分析:(1)连接AD,易证AD=BD,∠FAD=∠B=45°,即可证明△AFD≌△BED,可得DF=DE,∠ADF=∠BDE,即可求得∠EDF=90°,即可解题;
(2)根据△AFD≌△BED可得S△AFD=S△BED,即可解题.
(2)根据△AFD≌△BED可得S△AFD=S△BED,即可解题.
解答:证明:(1)连接AD,

∵等腰三角形ABC中,∠A=90°,D是斜边BC的中点,
∴AD=BD,∠FAD=∠B=45°,
在△AFD和△BED中,
,
∴△AFD≌△BED(SAS),
∴DF=DE,∠ADF=∠BDE,
∵∠ADE+∠BDE=90°,
∴∠ADF+∠ADE=90°,即∠EDF=90°,
∴△DEF是等腰直角三角形;
(2)∵△AFD≌△BED,
∴S△AFD=S△BED,
∴四边形AEDF的面积不变且等于S△ADB.

∵等腰三角形ABC中,∠A=90°,D是斜边BC的中点,
∴AD=BD,∠FAD=∠B=45°,
在△AFD和△BED中,
|
∴△AFD≌△BED(SAS),
∴DF=DE,∠ADF=∠BDE,
∵∠ADE+∠BDE=90°,
∴∠ADF+∠ADE=90°,即∠EDF=90°,
∴△DEF是等腰直角三角形;
(2)∵△AFD≌△BED,
∴S△AFD=S△BED,
∴四边形AEDF的面积不变且等于S△ADB.
点评:本题考查了全等三角形的判定,考查了全等三角形对应角相等的性质,考查了全等三角形面积相等的性质,本题中求证△AFD≌△BED是解题的关键.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
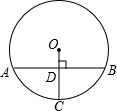 如图,在⊙O中,OC垂直弦AB于点D,交⊙O于点C,若AB=24,半径OC=13,则CD的长是
如图,在⊙O中,OC垂直弦AB于点D,交⊙O于点C,若AB=24,半径OC=13,则CD的长是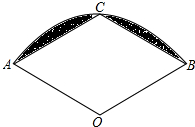 如图,在扇形AOB中,半径OA=1,∠AOB=120°,C为弧AB的中点,连接AC、BC,则图中阴影部分的面积是
如图,在扇形AOB中,半径OA=1,∠AOB=120°,C为弧AB的中点,连接AC、BC,则图中阴影部分的面积是