题目内容
4.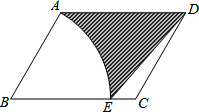 如图,在平行四边形ABCD中,AB=4,AD=5,∠B=60°,以点B为圆心,BA为半径作圆,交BC边于点E,连接ED,则图中阴影部分的面积为9$\sqrt{3}$-$\frac{8}{3}π$.
如图,在平行四边形ABCD中,AB=4,AD=5,∠B=60°,以点B为圆心,BA为半径作圆,交BC边于点E,连接ED,则图中阴影部分的面积为9$\sqrt{3}$-$\frac{8}{3}π$.
分析 过点A作AF⊥BC,易求平行四边形ABCD、扇形ABE、△DCE的面积,利用阴影部分的面积=平行四边形的面积-扇形面积-△DCE面积计算即可.
解答 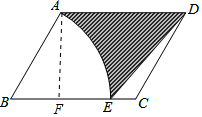 解:过点A作AF⊥BC,
解:过点A作AF⊥BC,
∵AB=4,∠B=60°,
∴AF=2$\sqrt{3}$,
∴平行四边形ABCD面积=BC•AF=10$\sqrt{3}$,
∵AB=BE=4,∠B=60°,
∴扇形ABE面积=$\frac{60π×{4}^{2}}{360}$=$\frac{8}{3}π$,
∵AD=BC=5,BE=4,
∴CE=1,
∴△DCE的面积=$\frac{1}{2}$CE•AF=$\sqrt{3}$,
∴阴影部分的面积=平行四边形的面积-扇形面积-△DCE面积=9$\sqrt{3}$-$\frac{8}{3}π$,
故答案为:9$\sqrt{3}$-$\frac{8}{3}π$.
点评 本题考查了平行四边形的性质、扇形的面积公式运用、三角形面积公式运用,解题的关键是作平行四边形的高线,构造直角三角形,并且求出其高线的长度.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.下面图形不是轴对称图形的是( )
| A. | 等腰三角形 | B. | 菱形 | C. | 平行四边形 | D. | 正六边形 |
15.下列运算正确的是( )
| A. | a3+a4=a7 | B. | (2a4)3=8a7 | C. | 2a3•a4=2a7 | D. | a8÷a2=a4 |
12.-$\frac{2}{5}$的绝对值是( )
| A. | $\frac{5}{2}$ | B. | -$\frac{5}{2}$ | C. | $\frac{2}{5}$ | D. | -$\frac{2}{5}$ |
16. 如图,已知DE∥BC,AB=AC,∠1=125°,则∠C的度数是( )
如图,已知DE∥BC,AB=AC,∠1=125°,则∠C的度数是( )
 如图,已知DE∥BC,AB=AC,∠1=125°,则∠C的度数是( )
如图,已知DE∥BC,AB=AC,∠1=125°,则∠C的度数是( )| A. | 55° | B. | 45° | C. | 35° | D. | 65° |
 二次函数y=ax2+bx+c(a≠0)的图象如图,若|ax2+bx+c|=k(k≠0)有两个不相等的实数根,则k的取值范围是k>3.
二次函数y=ax2+bx+c(a≠0)的图象如图,若|ax2+bx+c|=k(k≠0)有两个不相等的实数根,则k的取值范围是k>3.