题目内容
9.化简:(1)(x-1)(x+2)+(2x-1)(x+5)-x(2x-5);
(2)($\frac{x}{x-1}$-$\frac{x}{{x}^{2}-1}$)÷$\frac{{x}^{2}-x}{{x}^{2}-2x+1}$-$\frac{1}{x-1}$.
分析 (1)原式利用多项式乘以多项式,以及单项式乘以多项式法则计算,去括号合并即可得到结果;
(2)原式第一项括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分后两项通分并利用同分母分式的减法法则计算即可得到结果.
解答 解:(1)原式=x2+2x-x-2+2x2+10x-x-5-2x2+5x=x2+15x-7;
(2)原式=$\frac{x(x+1)-x}{(x+1)(x-1)}$•$\frac{(x-1)^{2}}{x(x-1)}$-$\frac{1}{x-1}$=$\frac{x}{x+1}$-$\frac{1}{x-1}$=$\frac{{x}^{2}-x-x-1}{{x}^{2}-1}$=$\frac{{{x^2}-2x-1}}{{{x^2}-1}}$.
点评 此题考查了分式的混合运算,以及整式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
19.下列手机软件图标中,是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
20.菱形的对角线长为8cm和6cm,则该菱形面积为( )
| A. | 48cm2 | B. | 24cm2 | C. | 25cm2 | D. | 14cm2 |
4.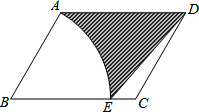 如图,在平行四边形ABCD中,AB=4,AD=5,∠B=60°,以点B为圆心,BA为半径作圆,交BC边于点E,连接ED,则图中阴影部分的面积为9$\sqrt{3}$-$\frac{8}{3}π$.
如图,在平行四边形ABCD中,AB=4,AD=5,∠B=60°,以点B为圆心,BA为半径作圆,交BC边于点E,连接ED,则图中阴影部分的面积为9$\sqrt{3}$-$\frac{8}{3}π$.
 如图,在平行四边形ABCD中,AB=4,AD=5,∠B=60°,以点B为圆心,BA为半径作圆,交BC边于点E,连接ED,则图中阴影部分的面积为9$\sqrt{3}$-$\frac{8}{3}π$.
如图,在平行四边形ABCD中,AB=4,AD=5,∠B=60°,以点B为圆心,BA为半径作圆,交BC边于点E,连接ED,则图中阴影部分的面积为9$\sqrt{3}$-$\frac{8}{3}π$.
19.关于x的不等式组$\left\{\begin{array}{l}{5-2x≥-1}\\{x-a>0}\end{array}\right.$的正整数解为2和3,则a的取值范围是( )
| A. | a≤2 | B. | 1≤a≤2 | C. | 1≤a<2 | D. | a≥1 |
 如图,直线a与直线b交于点A,与直线c交于点B,∠1=120°,∠2=45°,若使直线b与直线c平行,则可将直线b绕点A逆时针旋转15°.
如图,直线a与直线b交于点A,与直线c交于点B,∠1=120°,∠2=45°,若使直线b与直线c平行,则可将直线b绕点A逆时针旋转15°. 甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发驶向乙地.如图,线段OA和折线BCD分别表示货车和轿车离甲地距离y(千米)与车行驶时间x(小时)之间的函数关系.请根据图象解答下列问题:
甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发驶向乙地.如图,线段OA和折线BCD分别表示货车和轿车离甲地距离y(千米)与车行驶时间x(小时)之间的函数关系.请根据图象解答下列问题: