Question

已知直线m∥n，点C是直线m上一点，点D是直线n上一点，CD与直线m、n不垂直，点P为线段CD的中点．

（1）操作发现：直线l⊥m，l⊥n，垂足分别为A、B，当点A与点C重合时（如图①所示），连接PB，请直接写出线段PA与PB的数量关系：　PA=PB　．

（2）猜想证明：在图①的情况下，把直线l向上平移到如图②的位置，试问（1）中的PA与PB的关系式是否仍然成立？若成立，请证明；若不成立，请说明理由．

（3）延伸探究：在图②的情况下，把直线l绕点A旋转，使得∠APB=90°（如图③所示），若两平行线m、n之间的距离为2k．求证：PA•PB=k•AB．

 

Answer 1

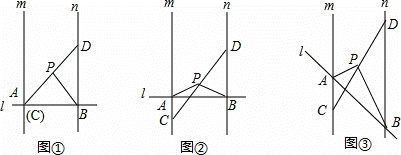
解：（1）∵l⊥n，

∴BC⊥BD，

∴三角形CBD是直角三角形，

又∵点P为线段CD的中点，

∴PA=PB．

（2）把直线l向上平移到如图②的位置，PA=PB仍然成立，理由如下：

如图②，过C作CE⊥n于点E，连接PE，

，

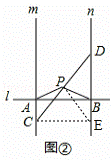∵三角形CED是直角三角形，点P为线段CD的中点，

∴PD=PE，

又∵点P为线段CD的中点，

∴PC=PD，

∴PC=PE；

∵PD=PE，

∴∠CDE=∠PEB，

∵直线m∥n，

∴∠CDE=∠PCA，

∴∠PCA=∠PEB，

又∵直线l⊥m，l⊥n，CE⊥m，CE⊥n，

∴l∥CE，

∴AC=BE，

在△PAC和△PBE中，

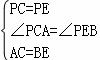
∴△PAC∽△PBE，

∴PA=PB．

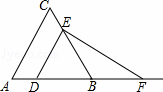
（3）如图③，延长AP交直线n于点F，作AE⊥BD于点E，

，

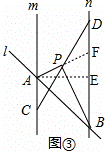∵直线m∥n，

∴，

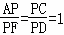∴AP=PF，

∵∠APB=90°，

∴BP⊥AF，

又∵AP=PF，

∴BF=AB；

在△AEF和△BPF中，

∴△AEF∽△BPF，

∴，

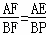∴AF•BP=AE•BF，

∵AF=2PA，AE=2k，BF=AB，

∴2PA•PB=2k．AB，

∴PA•PB=k•AB．

故答案为：PA=PB．