题目内容
如图,已知△ABC为等边三角形,AB=2,点D为边AB上一点,过点D作DE∥AC,交BC于E点;过E点作EF⊥DE,交AB的延长线于F点.设AD=x,△DEF的面积为y,则能大致反映y与x函数关系的图象是( )
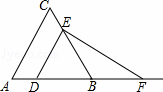
|
| A. |
| B. |
| C. |
| D. |
|
A解:∵△ABC是等边三角形,
∴∠B=60°,
∵DE∥AB,
∴∠EDC=∠B=60°,
∵EF⊥DE,
∴∠DEF=90°,
∴∠F=90°﹣∠EDC=30°;
∵∠ACB=60°,∠EDC=60°,
∴△EDC是等边三角形.
∴ED=DC=2﹣x,
∵∠DEF=90°,∠F=30°,
∴EF= ED=
ED= (2﹣x).
(2﹣x).
∴y= ED•EF=
ED•EF= (2﹣x)•
(2﹣x)• (2﹣x),
(2﹣x),
即y= (x﹣2)2,(x<2),
(x﹣2)2,(x<2),

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列命题是真命题的是( )
|
| A. | 一组对边平行,另一组对边相等的四边形是平行四边形 |
|
| B. | 对角线互相垂直的平行四边形是矩形 |
|
| C. | 四条边相 |
|
| D. | 正方形是轴对称图形,但不是中心对称图形 |




 等的四边形是菱形
等的四边形是菱形
 的解为
的解为 
 的解是
的解是  的定义域为___________.
的定义域为___________.