题目内容
14.先化简,再求值:[(2x-y)2+(2x-y)(2x+y)+4xy]÷4x,其中x=-$\frac{1}{2}$,y=4.分析 先算乘法,再合并同类项,算除法,最后代入求出即可.
解答 解:[(2x-y)2+(2x-y)(2x+y)+4xy]÷4x
=[4x2-4xy+y2+4x2-y2+4xy]÷4x
=8x2÷4x
=2x,
当x=-$\frac{1}{2}$,y=4时,原式=-1.
点评 本题考查了整式的混合运算和求值的应用,能运用整式的运算法则进行化简是解此题的关键,难度适中.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
4.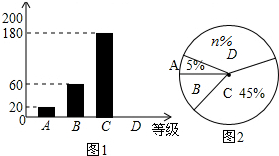 据报道:“国际剪刀石头布协会”提议将“剪刀石头布”作为奥运会比赛项目.为了调查学生对这个提议的了解程度,某校在学生中做了一次抽样调查,调查结果共分为四个等级:A、非常了解;B、比较了解;C、基本了解;D、不了解.根据调查统计结果,绘制了不完整的三种统计图表,请结合统计图表,回答下列问题:
据报道:“国际剪刀石头布协会”提议将“剪刀石头布”作为奥运会比赛项目.为了调查学生对这个提议的了解程度,某校在学生中做了一次抽样调查,调查结果共分为四个等级:A、非常了解;B、比较了解;C、基本了解;D、不了解.根据调查统计结果,绘制了不完整的三种统计图表,请结合统计图表,回答下列问题:
(1)本次参与调查的学生共有400人,m=15%,n=35.
(2)图2所示的扇形统计图中D部分扇形所对应的圆心角是126度;
(3)请补全图1示数的条形统计图;
(4)根据调查结果,学校准备开展关于“剪刀石头布”知识竞赛,某班要从“非常了解”态度的小明和小刚中选一人参加,现设计了如下游戏来确定,具体规则是:把四个完全相同的乒乓球标上数字1,2,3,4,然后放到一个不透明的袋中,一个人先从袋中随机摸出一个球,另一人再从剩下的三个球中随机摸出一个球,若摸出的两个求上的数字和为奇数,则小明去;否则小刚去,请用树状图或列表法说明这个游戏规则是否公平.
 据报道:“国际剪刀石头布协会”提议将“剪刀石头布”作为奥运会比赛项目.为了调查学生对这个提议的了解程度,某校在学生中做了一次抽样调查,调查结果共分为四个等级:A、非常了解;B、比较了解;C、基本了解;D、不了解.根据调查统计结果,绘制了不完整的三种统计图表,请结合统计图表,回答下列问题:
据报道:“国际剪刀石头布协会”提议将“剪刀石头布”作为奥运会比赛项目.为了调查学生对这个提议的了解程度,某校在学生中做了一次抽样调查,调查结果共分为四个等级:A、非常了解;B、比较了解;C、基本了解;D、不了解.根据调查统计结果,绘制了不完整的三种统计图表,请结合统计图表,回答下列问题:| 对提议的了解程度 | 百分比 |
| A、非常了解 | 5% |
| B、比较了解 | m |
| C、基本了解 | 45% |
(2)图2所示的扇形统计图中D部分扇形所对应的圆心角是126度;
(3)请补全图1示数的条形统计图;
(4)根据调查结果,学校准备开展关于“剪刀石头布”知识竞赛,某班要从“非常了解”态度的小明和小刚中选一人参加,现设计了如下游戏来确定,具体规则是:把四个完全相同的乒乓球标上数字1,2,3,4,然后放到一个不透明的袋中,一个人先从袋中随机摸出一个球,另一人再从剩下的三个球中随机摸出一个球,若摸出的两个求上的数字和为奇数,则小明去;否则小刚去,请用树状图或列表法说明这个游戏规则是否公平.
2.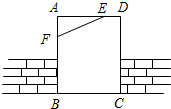 如图,工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变形,这样做的根据是( )
如图,工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变形,这样做的根据是( )
 如图,工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变形,这样做的根据是( )
如图,工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变形,这样做的根据是( )| A. | 两点之间,线段最短 | B. | 直角三角形的两个锐角互余 | ||
| C. | 三角形三个内角和等于180° | D. | 三角形具有稳定性 |
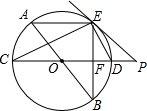 如图,AB、CD为⊙O的直径,弦AE∥CD,连接BE交CD于点F,过点E作直线EP与CD的延长线交于点P,使∠PED=∠C.
如图,AB、CD为⊙O的直径,弦AE∥CD,连接BE交CD于点F,过点E作直线EP与CD的延长线交于点P,使∠PED=∠C. 如图,在△ABC中,∠ABC和∠ACB的平分线交于点D,过点D作EF∥BC交AB于E 交AC于F,若AB=10,BC=7,AC=8,则△AEF的周长为( )
如图,在△ABC中,∠ABC和∠ACB的平分线交于点D,过点D作EF∥BC交AB于E 交AC于F,若AB=10,BC=7,AC=8,则△AEF的周长为( )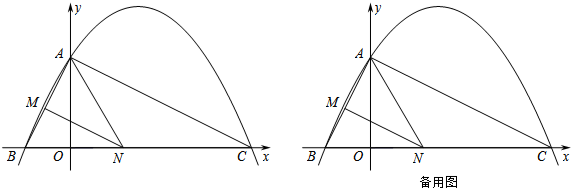
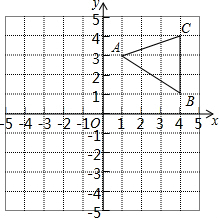 如图,已知△ABC三个顶点坐标分别是A(1,3),B(4,1),C(4,4).
如图,已知△ABC三个顶点坐标分别是A(1,3),B(4,1),C(4,4).