题目内容
若实数满足（x2+2x）+2（x2+2x）-3=0，则x2+2x的结果为 ．
考点：换元法解一元二次方程
专题：
分析：设x2+2x=t，则原方程转化为关于t的一元二次次方程，通过解方程求得t的值，即x2+2x的值．
解答：解：设x2+2x=t，则
t2+2t-3=0，
整理 得（t+3）（t-1）=0，
解得 t1=-3，t2=1，
即x2+2x=-3或x2+2x=1．
故答案是：-3或1．
t2+2t-3=0，
整理 得（t+3）（t-1）=0，
解得 t1=-3，t2=1，
即x2+2x=-3或x2+2x=1．
故答案是：-3或1．
点评：本题主要考查了换元法，即把某个式子看作一个整体，用一个字母去代替它，实行等量替换．
练习册系列答案
相关题目
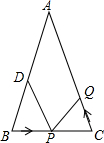如图，在△ABC中，AB=AC=10厘米，∠B=∠C，BC=8厘米，点D为AB的中点，如果点P在线段BC上以3厘米/秒的速度由B点向C点运动，同时点Q在线段CA上由C点向A点运动，当一个点停止运动时，另一个点也随之停止运动，当点Q的运动速度为
如图，△ABC的周长为28cm，把△ABC的边AC对折，使顶点C和点A重合，折痕交BC边于点D，交AC边于点E，连接AD．若AE=4cm，则△ABD的周长是将一元二次方程x2-6x-4=0化成（x+a）2=b的形式，则b等于（ ）
| A、3 | B、4 | C、7 | D、13 |