��Ŀ����
��֪��������y = x2+(2m��1)x + m2��1��������ԭ�㣬�ҵ�x < 0ʱ��y��x���������С.
(1)�������ߵĽ���ʽ����д��y < 0ʱ����Ӧx��ȡֵ��Χ;
(2)���A�Ǹ���������λ��x���·���һ�����㣬����A��x���ƽ���߽�����������һ��D������AB��x���ڵ�B�� DC��x���ڵ�C. �ٵ�BC=1ʱ��ֱ��д������ABCD���ܳ�;
���趯��A������Ϊ (a��b)��������ABCD���ܳ�L��ʾΪa�ĺ�����д���Ա�����ȡֵ��Χ���ж��ܳ��Ƿ�������ֵ��������ڣ����������ֵ���������ʱ��A������;��������ڣ���˵������.
�⣺(1)�������߾�������ԭ��(0,0)
��m2��1=0
��m = ��1
��y = x2+x��y = x2��3x��
��x<0ʱ��y��x���������С
�� y = x2��3x��
��ͼ��֪��y<0ʱ��0<x<3��
(2)�ٵ�BC=1ʱ,�������ߵĶԳ���֪��B��������Ϊ��2�����Ծ��ε��ܳ�Ϊ6 ��
(3)�ڡߵ�A������Ϊ��a��b��
�൱��A�ڶԳ������ʱ,����ABCD��һ��BC=3��2a����һ��AB=3a��a2
�ܳ�L=��2a2+2a+6 ,���� 0��a��
����A�ڶԳ����Ҳ�ʱ,���ε�һ��BC=3��(6��2a)=2a��3, ��һ��AB=3a��a2
�ܳ�L=��2a2+10a��6������ ��a��3
��a��3
�൱0��a�� ʱ��L=��2(a��
ʱ��L=��2(a��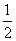 )2+
)2+ �൱a =
�൱a = 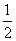 ʱ��L���=
ʱ��L���=  ��A������Ϊ(
��A������Ϊ(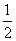 ,��
,�� )
)
�� ��a��3ʱ��L=��2(a��
��a��3ʱ��L=��2(a�� )2+
)2+  �൱a =
�൱a =  ʱ��L���=
ʱ��L���=  ��A������Ϊ(
��A������Ϊ( ,��
,�� )
)

 ��������ϵ�д�
��������ϵ�д� ��B��
��B��
 ��D��
��D��
 ��ͼ���ھ���ABCD�У���F�ڱ�BC�ϣ���AF=AD������D��DE��AF������Ϊ��E��
��ͼ���ھ���ABCD�У���F�ڱ�BC�ϣ���AF=AD������D��DE��AF������Ϊ��E�� �ij���
�ij���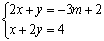 �Ľ�����x + y >��
�Ľ�����x + y >��
 B��
B��
 D��
D��
 B��
B�� C��0 D��
C��0 D��