题目内容
3. 如图,点A的坐标为(-8,0),点P的坐标为$({-\frac{7}{4},0})$,直线y=$\frac{3}{4}$x+b过点A,交y轴于点B,以点P为圆心,以PA为半径的圆交x轴于点C.
如图,点A的坐标为(-8,0),点P的坐标为$({-\frac{7}{4},0})$,直线y=$\frac{3}{4}$x+b过点A,交y轴于点B,以点P为圆心,以PA为半径的圆交x轴于点C.(1)判断点B是否在⊙P上?说明理由.
(2)求过A、B、C三点的抛物线的解析式;并求抛物线与⊙P另外一个交点为D的坐标.
(3)⊙P上是否存在一点Q,使以A、P、B、Q为顶点的四边形是菱形?若存在,求出点Q的坐标;若不存在,请说明理由.
分析 (1)把A(-8,0)代入y=$\frac{3}{4}$x+b得到点B(0,6),即OB=6,根据勾股定理即可得到结论;
(2)AC=2PA=$\frac{25}{2}$,则OC=$\frac{9}{2}$,点C$({\frac{9}{2},0})$,得到抛物线的解析式为y=-$\frac{1}{6}$x2-$\frac{7}{12}$x+6,直线x=$-\frac{7}{4}$是抛物线和圆P的对称轴,于是得到结论;
(3)当点Q在⊙P上时,有PQ=PA=$\frac{25}{4}$,如图1所示,假设AB为菱形的对角线,如图2所示,假设AB、AP为菱形的邻边,如图3所示,假设 AB、BP为菱形的邻边,于是得到结论.
解答  解:(1)∵A(-8,0)在直线y=$\frac{3}{4}$x+b上,则有b=6,
解:(1)∵A(-8,0)在直线y=$\frac{3}{4}$x+b上,则有b=6,
∴点B(0,6),即OB=6,
在Rt△BOP中,由勾股定理得PB=$\sqrt{O{P^2}+O{B^2}}=\frac{25}{4}$,则PB=PA,
∴点B在⊙P上;
(2)AC=2PA=$\frac{25}{2}$,则OC=$\frac{9}{2}$,点C$({\frac{9}{2},0})$,
抛物线过点A、C,则设所求抛物线为y=a(x+8)(x-$\frac{9}{2}$),代入点C$({\frac{9}{2},0})$,则有a=$-\frac{1}{6}$,
抛物线的解析式为y=-$\frac{1}{6}$x2-$\frac{7}{12}$x+6,
直线x=$-\frac{7}{4}$是抛物线和圆P的对称轴,点B的对称点为D,由对称可得D$({-\frac{7}{2},6})$;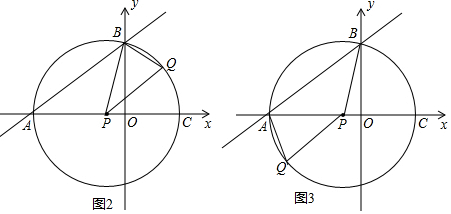
(3)当点Q在⊙P上时,有PQ=PA=$\frac{25}{4}$,
如图1所示,假设AB为菱形的对角线,那么PQ⊥AB且互相平分,由勾股定理得PE=$\frac{15}{4}$,则2PE≠PQ,所以四边形APBQ不是菱形.
如图2所示,假设AB、AP为菱形的邻边,则AB≠AP,所以四边形APQB不是菱形.
如图3所示,假设 AB、BP为菱形的邻边,则AB≠BP,所以四边形AQPB不是菱形.
综上所述,⊙P上不存在点Q,使以A、P、B、Q为顶点的四边形.
点评 本题考查了待定系数法求函数的解析式,菱形 的判定定理,对称的性质,正确的作出图形是解题的关键.

| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
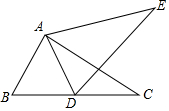 如图,将△ABC绕点A逆时针旋转50°得到△ADE,其中点D恰好落在BC边上,则∠EDC等于( )
如图,将△ABC绕点A逆时针旋转50°得到△ADE,其中点D恰好落在BC边上,则∠EDC等于( )| A. | 40° | B. | 50° | C. | 60° | D. | 65° |
| A. | 1 | B. | 6 | C. | 1或6 | D. | 5或6 |
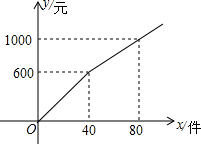 梅梅以每件6元的价格购进某商品若干件到市场去销售,销售金额y(元)与销售量x(件)的函数关系的图象如图所示,则降价后每件商品销售的价格为( )
梅梅以每件6元的价格购进某商品若干件到市场去销售,销售金额y(元)与销售量x(件)的函数关系的图象如图所示,则降价后每件商品销售的价格为( )| A. | 5元 | B. | 15元 | C. | 12.5元 | D. | 10元 |
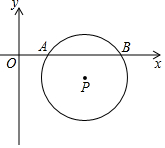 如图,平面直角坐标系中,⊙P与x轴分别交于A、B两点,点P的坐标为(3,-1),AB=2$\sqrt{3}$.将⊙P向上平移,当⊙P与x轴相切时平移的距离是( )
如图,平面直角坐标系中,⊙P与x轴分别交于A、B两点,点P的坐标为(3,-1),AB=2$\sqrt{3}$.将⊙P向上平移,当⊙P与x轴相切时平移的距离是( )| A. | 1 | B. | $\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | 3 |
 如图,已知A(-4,n),B(2,-4)是一次函数y=kx+b和反比例函数y=$\frac{m}{x}$的图象的两个交点.
如图,已知A(-4,n),B(2,-4)是一次函数y=kx+b和反比例函数y=$\frac{m}{x}$的图象的两个交点.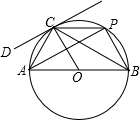 如图,点C是半径长为3的⊙O上任意一点,AB为直径,AC=3,过点C作⊙O的切线DC,点P为⊙O优弧AC上不与A、C重合的一个动点,点P从点C出发以每秒π个单位的速度顺时针匀速运动,到达点A停止运动.
如图,点C是半径长为3的⊙O上任意一点,AB为直径,AC=3,过点C作⊙O的切线DC,点P为⊙O优弧AC上不与A、C重合的一个动点,点P从点C出发以每秒π个单位的速度顺时针匀速运动,到达点A停止运动.