题目内容
已知OA⊥OB，∠AOB：∠AOC=3：4，则∠BOC的度数为（ ）
| A、30° |
| B、150° |
| C、30°或150° |
| D、不同于以上答案 |
考点：垂线
专题：
分析：根据垂直关系可得∠AOB=90°，再由∠AOB：∠AOC=3：4，可得∠AOC=120°，然后再分两种情况进行计算即可．
解答：
解：∵OA⊥OB，
∴∠AOB=90°，
∵∠AOB：∠AOC=3：4，
∴∠AOC=120°．
因为∠AOC的位置有两种：一种是在∠AOB在∠AOC内，一种是在∠AOC外．
①∠BOC=120°-90°=30°；
②∠BOC=360°-90°-120°=150°．
故选：C．
解：∵OA⊥OB，∴∠AOB=90°，
∵∠AOB：∠AOC=3：4，
∴∠AOC=120°．
因为∠AOC的位置有两种：一种是在∠AOB在∠AOC内，一种是在∠AOC外．
①∠BOC=120°-90°=30°；
②∠BOC=360°-90°-120°=150°．
故选：C．
点评：此题主要考查了垂线的定义：当两条直线相交所成的四个角中，有一个角是直角时，即两条直线互相垂直．同时做这类题时一定要结合图形．
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
下列运算正确的是（ ）
| A、（x3）2=x5 |
| B、a8÷a2=a6 |
| C、y4÷y4=0 |
| D、3m+3n=6mn |
若两圆的半径分别为5cm和8cm，圆心距为3cm，则这两个圆的位置关系是（ ）
| A、内切 | B、相交 | C、外切 | D、外离 |
下列运算正确的是（ ）
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
设a＞0，b＞0，c＞0，且
+
+
=3，则以下说法正确的是（ ）
| b |
| a |
| c |
| b |
| a |
| c |
| A、a，b，c可能相等，也可能不等 |
| B、a，b，c相等 |
| C、a，b，c不相等 |
| D、以上说法都不对 |
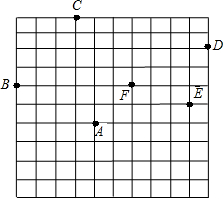如图，小蚂蚁在10×10的方格上沿着网格线运动（每小格边长为1），一只小蚂蚁在A处找到食物后，要通知B，C，D，E处的其他小蚂蚁，规定其行动为：向上或向右走为正，向下或向左走为负．如果从A到B记为：A→B（-4，+2）；从B到C记为：B→C（+3，+4）（第一个数表示左、右运动，第二个数表示上、下运动），那么：
已知有理数a，b，c，如图数轴所示，在数轴上标出表示-a，-b，-c的点，并比较a，-a，b，-b，c，-c，0的大小，并用符号“＜”连接起来．