题目内容
⊙O1与⊙O2的半径为r1、r2(r1>r2),连心线O1O2的中点为D,且O1O2上有一点H,满足2DH•O1O2=r12-r22,过H作垂直于O1O2的直线l,证明直线l上任一点M向两圆所引切线长相等.(两圆相离)
考点:切线的性质,勾股定理,圆与圆的位置关系
专题:证明题
分析:过直线l上任一点M向⊙O1和⊙O2引切线MN、ME,切点分别为N、E,如图,连接O1N,O1M,MO2,O2E,根据切线的性质得O1N⊥MN,在Rt△O1NM,利用勾股定理得MN2=O1M2-O1N2,在Rt△O1MH,利用勾股定理得O1M2=MH2+O1H2,则MN2=MH2+O1H2-r12=,由于O1H=
O1O2+DH,所以MN2=MH2+(
O1O2+DH)2-r12,
同理可得ME2=MH2+(
O1O2-DH)2-r22,则MN2-ME2=O1H2-r12=2O1D•DH-r12+r22,然后利用2DH•O1O2=r12-r22即可得到MN=ME.
| 1 |
| 2 |
| 1 |
| 2 |
同理可得ME2=MH2+(
| 1 |
| 2 |
解答: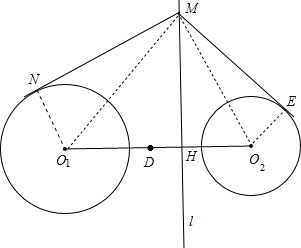 证明:过直线l上任一点M向⊙O1和⊙O2引切线MN、ME,切点分别为N、E,如图,
证明:过直线l上任一点M向⊙O1和⊙O2引切线MN、ME,切点分别为N、E,如图,
连接O1N,O1M,MO2,O2E,
∵MN为⊙O1的切线,
∴O1N⊥MN,
在Rt△O1NM,MN2=O1M2-O1N2,
在Rt△O1MH,O1M2=MH2+O1H2,
∴MN2=MH2+O1H2-r12=MH2+(O1D+DH)2-r12=MH2+(
O1O2+DH)2-r12,
同理可得ME2=MH2+(
O1O2-DH)2-r22,
∴MN2-ME2=O1H2-r12=2O1D•DH-r12+r22,
∵2DH•O1O2=r12-r22,
∴MN2-ME2=0,
∴MN=ME,
即直线l上任一点M向两圆所引切线长相等.
 证明:过直线l上任一点M向⊙O1和⊙O2引切线MN、ME,切点分别为N、E,如图,
证明:过直线l上任一点M向⊙O1和⊙O2引切线MN、ME,切点分别为N、E,如图,连接O1N,O1M,MO2,O2E,
∵MN为⊙O1的切线,
∴O1N⊥MN,
在Rt△O1NM,MN2=O1M2-O1N2,
在Rt△O1MH,O1M2=MH2+O1H2,
∴MN2=MH2+O1H2-r12=MH2+(O1D+DH)2-r12=MH2+(
| 1 |
| 2 |
同理可得ME2=MH2+(
| 1 |
| 2 |
∴MN2-ME2=O1H2-r12=2O1D•DH-r12+r22,
∵2DH•O1O2=r12-r22,
∴MN2-ME2=0,
∴MN=ME,
即直线l上任一点M向两圆所引切线长相等.
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了勾股定理和圆与圆的位置关系.

练习册系列答案
相关题目
近似数23.70所表示的准确数A的范围是( )
| A、23.65≤A<23.75 |
| B、23.60≤A<23.70 |
| C、23.695≤A<23.705 |
| D、23.700≤A<23.705 |
 如图,在等边△ABC中,E在BC的延长线上,CF平分∠ACE,P为射线BC上一点,Q为CF上一点,连接AP、PQ.若AP=PQ,求∠APQ是多少度.
如图,在等边△ABC中,E在BC的延长线上,CF平分∠ACE,P为射线BC上一点,Q为CF上一点,连接AP、PQ.若AP=PQ,求∠APQ是多少度.