题目内容
8.已知$\frac{x+2y}{3}$=$\frac{y+2z}{4}$=$\frac{z+2x}{5}$,则x:y:z=5:2:5.分析 设比值为k,然后列出关于x、y、z的三元一次方程组,再求解得到x、y、z,然后求出比值即可.
解答 解:设$\frac{x+2y}{3}$=$\frac{y+2z}{4}$=$\frac{z+2x}{5}$=k(k≠0),
则$\left\{\begin{array}{l}{x+2y=3k①}\\{y+2z=4k②}\\{z+2x=5k③}\end{array}\right.$,
①+②+③得,x+y+z=4k,
所以,x+y+z=y+2z,
所以,x=z,
代入③得,x+2x=5k,
解得x=$\frac{5}{3}$k,
将x=$\frac{5}{3}$k代入①得,$\frac{5}{3}$k+2y=3k,
解得y=$\frac{2}{3}$k,
所以,x:y:z=$\frac{5}{3}$k:$\frac{2}{3}$k:$\frac{5}{3}$k=5:2:5.
故答案为:5:2:5.
点评 本题考查了比例的性质,利用“设k法”求解更简便,本题难点在于求出x=z.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
19.六角螺母绕其中心至少旋转多少度,才能与它本身重合?( )
| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
13.在△ABC中,∠A=105°,∠B=45°,cosC的值是( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
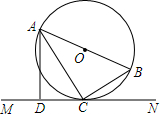 如图,AB是⊙O的直径,C是⊙O上的一点,直线MN经过点C,过点A作直线MN的垂线,垂足为点D,且AC平分∠BAD.
如图,AB是⊙O的直径,C是⊙O上的一点,直线MN经过点C,过点A作直线MN的垂线,垂足为点D,且AC平分∠BAD.