题目内容
20.化简:$\sqrt{\frac{5(a-b)}{27(a+b)}}$(a>b>0)分析 先由a>b>0,得到a-b>0,a+b>0,再根据二次根式的性质进行化简.
解答 解:∵a>b>0,
∴a-b>0,a+b>0,
$\sqrt{\frac{5(a-b)}{27(a+b)}}$=$\sqrt{\frac{5(a-b)×3(a+b)}{27(a+b)×3(a+b)}}=\frac{\sqrt{15({a}^{2}-{b}^{2})}}{9(a+b)}$.
点评 本题考查了二次根式的性质,解决本题的关键是熟记二次根式的性质.

练习册系列答案
相关题目
8.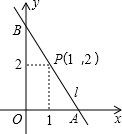 如图,直线l经过点P(1,2)与坐标轴交于A(a,0),B(0,b)两点(其中a<b),如果a+b=6,那么tan∠ABO的值为( )
如图,直线l经过点P(1,2)与坐标轴交于A(a,0),B(0,b)两点(其中a<b),如果a+b=6,那么tan∠ABO的值为( )
 如图,直线l经过点P(1,2)与坐标轴交于A(a,0),B(0,b)两点(其中a<b),如果a+b=6,那么tan∠ABO的值为( )
如图,直线l经过点P(1,2)与坐标轴交于A(a,0),B(0,b)两点(其中a<b),如果a+b=6,那么tan∠ABO的值为( )| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
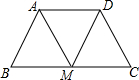 如图,已知AD∥BC,M是BC的中点,且MA=MD,求证:△ABM≌△DCM.
如图,已知AD∥BC,M是BC的中点,且MA=MD,求证:△ABM≌△DCM.