题目内容
 如图,一个长方形花坛的长AD为8米,一条对角线AC的长为10米.
如图,一个长方形花坛的长AD为8米,一条对角线AC的长为10米.(1)求这个花坛的周长;
(2)点B到AC的距离是多少?
考点:勾股定理的应用
专题:
分析:(1)直接利用勾股定理得出DC的长,进而求出矩形的周长即可;
(2)利用三角形面积公式得出B到AC的距离即可.
(2)利用三角形面积公式得出B到AC的距离即可.
解答: 解:(1)∵一个长方形花坛的长AD为8米,一条对角线AC的长为10米,
解:(1)∵一个长方形花坛的长AD为8米,一条对角线AC的长为10米,
∴在Rt△ADC中,
DC=
=6(m),
则这个花坛的周长为:2×(6+8)=28(m);
(2)过点B作BE⊥AC于点E,
可得:BE×AC=AB×BC,
则BE=
=
=4.8(m),
答:点B到AC的距离是4.8m.
 解:(1)∵一个长方形花坛的长AD为8米,一条对角线AC的长为10米,
解:(1)∵一个长方形花坛的长AD为8米,一条对角线AC的长为10米,∴在Rt△ADC中,
DC=
| AC2-AD2 |
则这个花坛的周长为:2×(6+8)=28(m);
(2)过点B作BE⊥AC于点E,
可得:BE×AC=AB×BC,
则BE=
| AB×BC |
| AC |
| 6×8 |
| 10 |
答:点B到AC的距离是4.8m.
点评:此题主要考查了勾股定理的应用以及三角形面积,熟练应用矩形的性质是解题关键.

练习册系列答案
相关题目

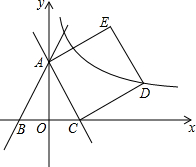 在平面直角坐标系中,直线y=2x+2分别与y轴,x轴交于点A,B两点,在x轴正半轴上取一点C,使OC=OB,以AC为边长在第一象限作正方形ACDE,顶点D恰好在反比例函数y=
在平面直角坐标系中,直线y=2x+2分别与y轴,x轴交于点A,B两点,在x轴正半轴上取一点C,使OC=OB,以AC为边长在第一象限作正方形ACDE,顶点D恰好在反比例函数y=
 已知CD⊥AB于D,BE⊥AC于E 求证:D,B,C,E在同一圆上.
已知CD⊥AB于D,BE⊥AC于E 求证:D,B,C,E在同一圆上.