题目内容
14.已知正比例函数y1=k1x的图象与一次函数y2=k2x-4的图象交于点P(1,-2).(1)求k1、k2的值;
(2)这两个函数图象与y轴所围成的三角形面积.
分析 (1)把P点坐标分别代入y1=k1x和y2=k2x-4中可求出k1、k2的值;
(2)先确定一次函数y2=k2x-4的图象与y轴的交点坐标,然后根据三角形面积公式计算即可.
解答 解:(1)把P(1,-2)代入y1=k1x得k1=-2;
把P(1,-2)代入y2=k2x-4得k2-4=-2,解得k2=2;
(2)当x=0时,y=2x-4=-4,则一次函数y2=k2x-4的图象与y轴的交点坐标为(0,-4),
所以这两个函数图象与y轴所围成的三角形面积=$\frac{1}{2}$×4×1=2.
点评 本题考查了两直线相交或平行问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解;若两条直线是平行的关系,那么它们的自变量系数相同,即k值相同.也考查了三角形面积公式.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
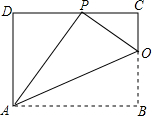 已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处.如图,已知折痕与边BC交于O,连结AP、OP、OA.
已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处.如图,已知折痕与边BC交于O,连结AP、OP、OA. 如图,正方形OABC绕着点O逆时针旋转40°得到正方形ODEF,连接AF,则∠OFA的度数是25°.
如图,正方形OABC绕着点O逆时针旋转40°得到正方形ODEF,连接AF,则∠OFA的度数是25°.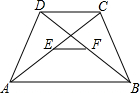 如图:AB∥CD,E,F分别是AC,DB的中点.
如图:AB∥CD,E,F分别是AC,DB的中点.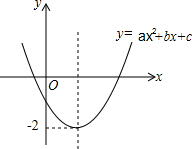 二次函数y=ax2+bx+c的图象如图.
二次函数y=ax2+bx+c的图象如图.