题目内容
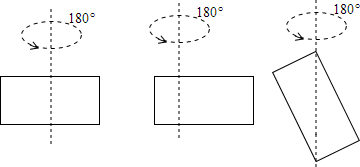
12. 如图,已知在?ABCD中,对角线AC和BD相交于点O,AC=10,BD=8,AC与BD的夹角∠AOD=60°,求?ABCD的面积.
如图,已知在?ABCD中,对角线AC和BD相交于点O,AC=10,BD=8,AC与BD的夹角∠AOD=60°,求?ABCD的面积.
分析 过点A分别作AE⊥BD,垂足为E,根据三角函数即可求得AE的长,从而求得△OAD的面积,四边形ABCD的面积是三角形OAD的面积的4倍,据此即可求解.
解答  解:过点A分别作AE⊥BD,垂足为E,
解:过点A分别作AE⊥BD,垂足为E,
∵四边形ABCD为平行四边形,
∴AO=CO=$\frac{1}{2}$AC=5,BO=DO=$\frac{1}{2}$BD=4,
在Rt△AOE中,sin∠AOE=$\frac{AE}{AO}$,
∴AE=AO•sin∠AOE=AO×sin60°=$\frac{5\sqrt{3}}{2}$,
∴SABCD=$\frac{1}{2}$OD•AE×4=$\frac{1}{2}$×4×$\frac{5\sqrt{3}}{2}$×4=20$\sqrt{3}$.
点评 本题主要考查了平行四边形性质,正确理解四边形ABCD的面积是△OAD的面积的4倍是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
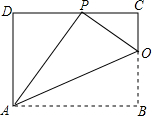 已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处.如图,已知折痕与边BC交于O,连结AP、OP、OA.
已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处.如图,已知折痕与边BC交于O,连结AP、OP、OA.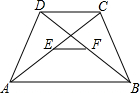 如图:AB∥CD,E,F分别是AC,DB的中点.
如图:AB∥CD,E,F分别是AC,DB的中点. 如图,OA、OB、OC都是⊙O的半径,∠AOB=2∠BOC,
如图,OA、OB、OC都是⊙O的半径,∠AOB=2∠BOC, 求如图所示的图形中小圆圈的总数.
求如图所示的图形中小圆圈的总数.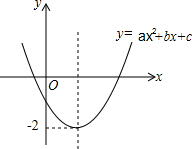 二次函数y=ax2+bx+c的图象如图.
二次函数y=ax2+bx+c的图象如图.