��Ŀ����
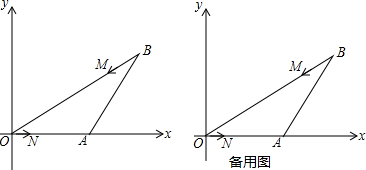
13����ͼ����ƽ��ֱ������ϵ�У���A��x���ϣ���OA=BA=2����OAB=120�㣬��N��O��������ÿ��1����λ���ٶ���O��A��B��B�˶�����M��B��������ÿ��$\sqrt{3}$����λ���ٶ���B��O��y���������˶���M��Nͬʱ����������N�����Bʱ����ͬʱֹͣ�˶������˶�ʱ��Ϊt����OMN�����ΪS����1�����B�����겢���ֱ��AB�Ľ���ʽ��
��2����ֱ��д��S��t�ĺ�����ϵʽ��д���Ա���t��ȡֵ��Χ��
��3������M���߶�BO���˶�ʱ����OMN�Ƿ���ܳ�Ϊ���������Σ�������ܣ������ʱt��ֵ��������ܣ���˵�����ɣ�
���� ��1������������Ǻ������ɵ�AD��BD�������߶εĺͲ�ɵ�B�����ꣻ���ݴ���ϵ�������ɵô𰸣�
��2���������ۣ��ٵ�0��t��2ʱ�������߶εĺͲ�ɵ�OM�ij�������������Ǻ������ɵ�M�������꣬���������ε������ʽ���ɵô𰸣��ڵ�2��t��4ʱ������������Ǻ������߶εĺͲ�ɵ�N��ĺ����꣬���������ε������ʽ���ɵô𰸣�
��3�����ݵ��������εĶ��壬�ɵù���t�ķ��̣����ݽⷽ�̣��ɵô𰸣�
��� �⣺��1����ͼ1��
��BD��OA��D�㣮
��OA=BA=2����OAB=120�㣬��
��BAD=60�㣮
AD=AB•cos��BAD=2��$\frac{1}{2}$=1��OD=OA+AD=3��
BD=ABisn��BAD=2��sin60��=2��$\frac{\sqrt{3}}{2}$=$\sqrt{3}$��
B��������3��$\sqrt{3}$����
��AB�Ľ���ʽΪy=kx+b����A��B��������룬��
$\left\{\begin{array}{l}{2k+b=0}\\{3k+b=\sqrt{3}}\end{array}\right.$��
���$\left\{\begin{array}{l}{k=\frac{\sqrt{3}}{3}}\\{b=-\frac{2\sqrt{3}}{3}}\end{array}\right.$��
ֱ��AB�Ľ���ʽΪy=$\frac{\sqrt{3}}{3}$x-$\frac{2\sqrt{3}}{3}$��
��2���ٵ�0��t��2ʱ��ON=t��BM=$\sqrt{3}$t��OM=2$\sqrt{3}$-$\sqrt{3}$t��
yM=OM•sin��BOA=��2$\sqrt{3}$-$\sqrt{3}$t��sin30��=$\sqrt{3}$-$\frac{\sqrt{3}}{2}$t��
S=$\frac{1}{2}$ON•yM=$\frac{1}{2}$•t•��$\sqrt{3}$-$\frac{\sqrt{3}}{2}$t��=-$\frac{\sqrt{3}}{4}$t2+$\frac{\sqrt{3}}{2}$t��
�ڵ�2��t��4ʱ��ON=t-2��OM=$\sqrt{3}$t-2$\sqrt{3}$��xN=��t-2��cos��BAD+2=$\frac{1}{2}$��t-2��+2=$\frac{1}{2}$t+1��
S=$\frac{1}{2}$OM•xN=$\frac{1}{2}$��$\sqrt{3}$t-2$\sqrt{3}$��•��$\frac{1}{2}$t+1��=$\frac{\sqrt{3}}{4}$t2-$\sqrt{3}$��
����������S=$\left\{\begin{array}{l}{-\frac{\sqrt{3}}{4}{t}^{2}+\frac{\sqrt{3}}{2}t��0��t��2��}\\{\frac{\sqrt{3}}{4}{t}^{2}-\sqrt{3}��2��t��4��}\end{array}\right.$��
��3��OM=2$\sqrt{3}$-$\sqrt{3}$t��ON=t��
��OM=ONʱ��2$\sqrt{3}$-$\sqrt{3}$t=t�����t=3-$\sqrt{3}$��
��ON=MNʱ��$\frac{OM}{OB}$=$\frac{ON}{OA}$����$\frac{2\sqrt{3}-\sqrt{3}t}{2\sqrt{3}}$=$\frac{t}{2}$�����t=1��
��OM=MNʱ��MO•cos��MON=$\frac{1}{2}$ON������2$\sqrt{3}$-$\sqrt{3}$t��cos30��=$\frac{1}{2}$t��
���t=$\frac{3}{2}$��
��������������M���߶�BO���˶�ʱ����OMN�ܳ�Ϊ���������Σ���ʱt��ֵt1=3-$\sqrt{3}$��t2=1��t3=$\frac{3}{2}$��
���� ���⿼����һ�κ����ۺ��⣬��1������������Ǻ������߶εĺͲ�ó�B�������ǽ���ؼ�����2������������Ǻ����ó�yM��xN�ǽ���ؼ�����3�����õ��������εĶ���ó�����t�ķ����ǽ���ؼ���Ҫ�������ۣ��Է���©��

| A�� | x+2y=0 | B�� | x2+3x+2=0 | C�� | 2x-3=$\frac{1}{x}$+2 | D�� | x+1=0 |
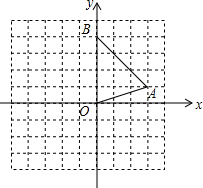 �ڡ�OAB�У���B�������ǣ�0��4������A�������ǣ�3��1����
�ڡ�OAB�У���B�������ǣ�0��4������A�������ǣ�3��1����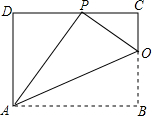 ��֪����ABCD��һ����AD=8��������ABCD�۵���ʹ�ö���B����CD���ϵ�P�㴦����ͼ����֪�ۺ����BC����O������AP��OP��OA��
��֪����ABCD��һ����AD=8��������ABCD�۵���ʹ�ö���B����CD���ϵ�P�㴦����ͼ����֪�ۺ����BC����O������AP��OP��OA��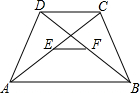 ��ͼ��AB��CD��E��F�ֱ���AC��DB���е㣮
��ͼ��AB��CD��E��F�ֱ���AC��DB���е㣮