Question

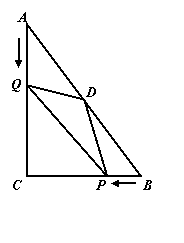
已知：如图，在ΔABC中，∠C=90°，AC=8cm，BC=6cm，D是斜边AB的中点．点P从点B出发沿BC^方向匀速运动，速度为1 cm/s；同时，点Q从点A出发，沿AC方向匀速运动，速度为2 cm/s.当点Q停止运动时，点P也停止运动.连接PQ、PD 、QD.设运动时间为t（s）（0＜t ＜4）．

（1）当t为何值时，ΔPQC是等腰直角三角形？

（2）设ΔPQD的面积为y （cm²），求y与t之间的函数关系式；是否存在某一时刻t，使ΔPQD的面积是RtΔABC的面积的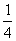？若存在，求出t的值；若不存在，请说明理由；

（3）是否存在某一时刻t，使QD⊥PD？若存在，求出t的值；若不存在，请说明理由．

 

Answer 1

解：（1）8－2t=6－t

t＝2 (秒)．…………………………………………3 分

（2）过Q作QF⊥AB，交AB于F，

Rt△AQF∽Rt△ABC

得

其中BC=6，AC=8，AB=10，AQ=2t

∴

同样可求得：

∴

…………………………………………………………6分

根据题意，    解得

答：当t=3秒或t=2秒时，ΔPQD的面积是RtΔABC的面积的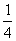. …………… 9分

（3）

同样可得:;

当PD⊥QD时，

此时，t＝ (秒)．

答：当t＝时，PD⊥QD．