题目内容
(1)已知a<0,化简
-
(2)a+
=4(0<a<1),则
-
= .
4-(a+
|
4+(a-
|
(2)a+
| 1 |
| a |
| a |
| 1 | ||
|
考点:二次根式的化简求值
专题:
分析:(1)把两个被开方数写成完全平方的形式,然后根据a的范围,确定a-
的符号,从而根据算术平方根的意义化简求值;
(2)把所求的式子进行平方,然后根据算术平方根的性质求解.
| 1 |
| a |
(2)把所求的式子进行平方,然后根据算术平方根的性质求解.
解答:解:(1)原式=
+
当a<-1时,a-
<0,a+
<0,则原式=
-a+(a+
)=
;
当-1≤a<0时,a-
≥0,a+
<0,则原式=a-
+(a+
)=2a;
(2)(
-
)2=a+
-2=4-2=2;
∵0<a<1,则
-
<0,
则原式=-
.
故答案是:-
.
(a-
|
(a+
|
当a<-1时,a-
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 2 |
| a |
当-1≤a<0时,a-
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
(2)(
| a |
| 1 | ||
|
| 1 |
| a |
∵0<a<1,则
| a |
| 1 | ||
|
则原式=-
| 2 |
故答案是:-
| 2 |
点评:此题主要考查的是二次根式的性质:
=-a(a≤0),正确根据字母的范围化简二次根式是关键.
| a2 |

练习册系列答案
 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
多项式-2a(x+y)3+6a2(x+y)的公因式是( )
| A、-2a2(x+y)2 |
| B、6a(x+y) |
| C、-2a(x+y) |
| D、-2a |
已知开口向上的抛物线y=ax2+bx+c经过点(4,-6)、(-2,0),与x轴交于点A、B两点,与y轴交于点C,则△ABC面积的最小值是( )
A、10+4
| ||
B、10-4
| ||
C、10+4
| ||
D、10-4
|
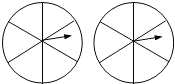 如图,用两个相同的转盘(每个圆都平均分成六个扇形)玩配紫色游戏(-个转盘转出“红”,另一个转盘转出“蓝”,则为配成紫色).在所给转盘中的扇形里,分别填上“红”或“蓝”,使得到紫色的概率是
如图,用两个相同的转盘(每个圆都平均分成六个扇形)玩配紫色游戏(-个转盘转出“红”,另一个转盘转出“蓝”,则为配成紫色).在所给转盘中的扇形里,分别填上“红”或“蓝”,使得到紫色的概率是 画出右上方图形关于直线l的对称图形.
画出右上方图形关于直线l的对称图形.