题目内容
15. 如图,Rt△ABC中,∠C=90°,AB=5,AC=3,现将△ABC绕着顶点B旋转,记点C的对应点为点C1,当点A,B,C1三点共线时,求∠BC1C的正切值=3或$\frac{1}{3}$.
如图,Rt△ABC中,∠C=90°,AB=5,AC=3,现将△ABC绕着顶点B旋转,记点C的对应点为点C1,当点A,B,C1三点共线时,求∠BC1C的正切值=3或$\frac{1}{3}$.
分析 作CE⊥AB垂足为E,根据题意有两种情形,分别在RT△CEC1和RT△CEC1′根据正切值的定义求出.
解答 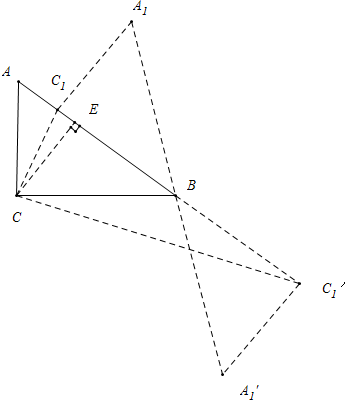 解:如图作CE⊥AB,垂足为E,
解:如图作CE⊥AB,垂足为E,
情形①当点C1在线段AB上时,
∵∠C=90°,AB=5,AC=3,
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∵$\frac{1}{2}$AB•CE=$\frac{1}{2}$AC•BC,
∴CE=$\frac{12}{5}$,
∴EB=$\sqrt{B{C}^{2}-C{E}^{2}}$=$\sqrt{{4}^{2}-(\frac{12}{5})^{2}}$=$\frac{16}{5}$,
∵BC=BC1,
∴EC1=BC1-EB=4-$\frac{16}{5}$=$\frac{4}{5}$,
∴tan∠BC1C=$\frac{EC}{E{C}_{1}}$=3.
情形②当C1′在AB的延长线上时,tan∠BC1′C=$\frac{EC}{E{C}_{1}′}$=$\frac{\frac{12}{5}}{4+\frac{16}{5}}$=$\frac{1}{3}$.
故答案为3或$\frac{1}{3}$.
点评 本题考查正切值的定义、勾股定理、旋转的有关概念,正确作出图形是解决问题的关键.

练习册系列答案
相关题目
19.下列长度的三条线段,能组成三角形的是( )
| A. | 3,6,9 | B. | 5,6,11 | C. | 5,6,10 | D. | 1,4,7 |
5.某厂生产A,B两种产品,其单价随市场变化而做相应调整,营销人员根据前四次单价变化的情况,绘制了如下统计表:
A,B产品单价变化统计表
并求得了A产品四次单价的平均数和方差:
$\overline{{x}_{A}}$=5.9,sA2=$\frac{1}{4}$[(6-5.9)2+(5.2-5.9)2+(6.5-5.9)2+(5.9-5.9)2]=$\frac{43}{200}$
(1)B产品第四次的单价比第二次的单价减少了12.5%;
(2)A产品四次单价的中位数是5.95;B产品四次单价的众数是3.5;
(3)求B产品四次单价的方差,并比较哪种产品的单价波动小.
A,B产品单价变化统计表
| 第一次 | 第二次 | 第三次 | 第四次 | |
| A产品单价(元/件) | 6 | 5.2 | 6.5 | 5.9 |
| B产品单价(元/件) | 3.5 | 4 | 3 | 3.5 |
$\overline{{x}_{A}}$=5.9,sA2=$\frac{1}{4}$[(6-5.9)2+(5.2-5.9)2+(6.5-5.9)2+(5.9-5.9)2]=$\frac{43}{200}$
(1)B产品第四次的单价比第二次的单价减少了12.5%;
(2)A产品四次单价的中位数是5.95;B产品四次单价的众数是3.5;
(3)求B产品四次单价的方差,并比较哪种产品的单价波动小.
 如图,在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC、AB分别交于点D、E,且∠CBD=∠A.
如图,在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC、AB分别交于点D、E,且∠CBD=∠A.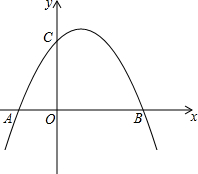 如图所示,抛物线y=ax2+x+c(a≠0)与x轴交于点A(-2,0)、点B(6,0),与y轴交于点C.
如图所示,抛物线y=ax2+x+c(a≠0)与x轴交于点A(-2,0)、点B(6,0),与y轴交于点C. 如图,在Rt△ABC中,∠A=90°,∠B=30°,AB=6,求BC.
如图,在Rt△ABC中,∠A=90°,∠B=30°,AB=6,求BC. 如图,该图形由6个完全相同的小正方形排列而成.
如图,该图形由6个完全相同的小正方形排列而成.