题目内容
7.如图1,已知抛物线y=ax2-$\frac{3}{2}$x+c与x轴相交于A、B两点,并与直线y=$\frac{1}{2}$x-2交于B、C两点,其中点C是直线y=x-2与y轴的交点,连接AC.(1)点B的坐标是(4,0);点C的坐标是(0,-2);
(2)求抛物线的解析式;
(3)设点E是线段CB上的一个动点(不与点B、C重合),直线EF∥y轴,交抛物线与点F,问点E运动到何处时,线段EF的长最大?并求出EF的长的最大值;
(4)如图2,点D是抛物线的顶点,判断直线CD是否是经过A、B、C三点的圆的切线,并说明理由.

分析 (1)先令x=0,y=0,求出点C,B坐标,
(2)把点C,B坐标代入抛物线求出a,c的值即可,
(3)由点在直线BC上设出点E的坐标,表示出线段EF的长度,运用二次函数最大值的知识求出点E的位置,
(4)先判断出AB是经过A、B、C三点的圆的直径,确定圆心,连接圆心和切点,证明垂直即可.
解答 解:(1)由题意知直线y=$\frac{1}{2}$x-2交x轴、y轴于点B、C两点,
∴B(4,0),C(0,-2),
(2)∵y=ax2-$\frac{3}{2}$x+c经过点B,C,
∴$\left\{\begin{array}{l}{0=16a-6+c}\\{-2=c}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{c=-2}\end{array}\right.$,
∴y=$\frac{1}{2}{x}^{2}-\frac{3}{2}x-2$;
(3)如图1: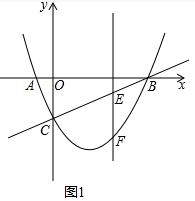
设点E(x,$\frac{1}{2}$x-2),
∵直线EF∥y轴,
∴点F(x,$\frac{1}{2}{x}^{2}-\frac{3}{2}x-2$),
EF=$\frac{1}{2}$x-2-($\frac{1}{2}{x}^{2}-\frac{3}{2}x-2$),
EF=$-\frac{1}{2}{x}^{2}+2x$=$-\frac{1}{2}(x-2)^{2}+2$,
所以当x=2时,EF有最大值是2,
此时E(2,-1),EF的最大值为2;
(4)如图2: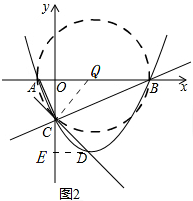
∵y=ax2-$\frac{3}{2}$x+c与x轴相交于A、B两点,
令y=0,得ax2-$\frac{3}{2}$x+c=0,
解得:x=-1,或x=4,
∴A(-1,0),B(4,0),C(0,-2),
∴OA=1,OC=2,0B=4,
∴tan∠ACO=tan∠CBO=$\frac{1}{2}$,
∴∠ACO=∠CBO,
∵∠OCB+∠CBO=90°,
∴∠ACO+∠OCB=90°,
∴∠ACB=90°,
∴AB是经过A、B、C三点的圆的直径,
设圆心Q,则Q($\frac{3}{2}$,0),连接QC,过点D作DE⊥y轴,垂足为E,连接QD,
y=$\frac{1}{2}{x}^{2}-\frac{3}{2}x-2$顶点坐标为D($\frac{3}{2}$,$-\frac{25}{8}$),
可求CE=-2-($-\frac{25}{8}$)=$\frac{9}{8}$,ED=$\frac{3}{2}$,CD=$\frac{15}{8}$,CQ=$\sqrt{O{C}^{2}+O{Q}^{2}}$=$\frac{5}{2}$,QD=$\frac{25}{8}$,
计算得:CD2+CQ2=DQ2,
∴∠QCD=90°,
∴直线CD是经过A、B、C三点的圆的切线.
点评 此题主要考查二次函数的综合问题,会求函数与坐标轴的交点,会用点的坐标表示线段长度,知道运用二次函数解决最值问题,熟悉圆的切线的证明是解题的关键.

 一个大正方形和四个全等的小正方形按图①、②两种方式摆放,则图②的大正方形中未被小正方形覆盖部分的面积为( )
一个大正方形和四个全等的小正方形按图①、②两种方式摆放,则图②的大正方形中未被小正方形覆盖部分的面积为( )| A. | a-b | B. | a+b | C. | ab | D. | a2-ab |
 如图,DE是△ABC边AB的垂直平分线,若BC=8cm,AC=10cm,则△DBC的周长为( )
如图,DE是△ABC边AB的垂直平分线,若BC=8cm,AC=10cm,则△DBC的周长为( )| A. | 16cm | B. | 18cm | C. | 30cm | D. | 2cm |
 大庆素有百湖之城的美称,如图所示.在临湖高出水面50米的塔AB顶层A处望见一艘飞艇停留在平静的湖面上空某处.观察到艇底部醒目标志阳目志P处的仰角为45°,又观察到其在湖中的影像的俯角为60°,试求飞艇距湖面的高度h(结果可用含根号的式子表示).
大庆素有百湖之城的美称,如图所示.在临湖高出水面50米的塔AB顶层A处望见一艘飞艇停留在平静的湖面上空某处.观察到艇底部醒目标志阳目志P处的仰角为45°,又观察到其在湖中的影像的俯角为60°,试求飞艇距湖面的高度h(结果可用含根号的式子表示).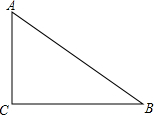 如图,Rt△ABC中,∠C=90°,AB=5,AC=3,现将△ABC绕着顶点B旋转,记点C的对应点为点C1,当点A,B,C1三点共线时,求∠BC1C的正切值=3或$\frac{1}{3}$.
如图,Rt△ABC中,∠C=90°,AB=5,AC=3,现将△ABC绕着顶点B旋转,记点C的对应点为点C1,当点A,B,C1三点共线时,求∠BC1C的正切值=3或$\frac{1}{3}$.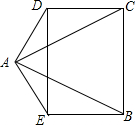 如图,AB=AC,AD=AE,∠DAB=∠EAC,DE=CB.
如图,AB=AC,AD=AE,∠DAB=∠EAC,DE=CB. 如图,已知二次函数y=ax2-4x+c的图象经过点A(-1,0)和点D(5,0).
如图,已知二次函数y=ax2-4x+c的图象经过点A(-1,0)和点D(5,0).
 将下列选项中的平面图形绕直线l旋转一周,可得到如图所示立体图形( )
将下列选项中的平面图形绕直线l旋转一周,可得到如图所示立体图形( )


