题目内容
14.函数y=$\sqrt{{x}^{2}+2x+5}$+$\sqrt{{x}^{2}-4x+5}$的最小值为3$\sqrt{2}$.分析 把原式化为y=$\sqrt{(x+1)^{2}+(0-2)^{2}}$+$\sqrt{(x-2)^{2}+(0-1)^{2}}$,y 为 动点(x,0)到 A(-1,2)和B(2,1)的距离之和,作点A关于x轴对称点点C(-1,-2),连接BC交x轴于点D,D点坐标即为所求的x,求出直线BC的解析式,并求出与x轴的交点的横坐标,代入原式即可.
解答  解:∵y=$\sqrt{{x}^{2}+2x+5}$+$\sqrt{{x}^{2}-4x+5}$=$\sqrt{(x+1)^{2}+(0-2)^{2}}$+$\sqrt{(x-2)^{2}+(0-1)^{2}}$,
解:∵y=$\sqrt{{x}^{2}+2x+5}$+$\sqrt{{x}^{2}-4x+5}$=$\sqrt{(x+1)^{2}+(0-2)^{2}}$+$\sqrt{(x-2)^{2}+(0-1)^{2}}$,
∴y 为 动点(x,0)到 A(-1,2)和B(2,1)的距离之和,
作点A关于x轴对称点点C(-1,-2),连接BC交x轴于点D,
D点坐标即为所求的x,
设直线BC的解析式为:y=kx+b,
把B,C的坐标代入得:$\left\{\begin{array}{l}{-2=-k+b}\\{1=2k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=1}\\{b=-1}\end{array}\right.$,
∴y=x-1,
令y=0,则x=1,
把x=1代入原式得 最小值为$\sqrt{8}$+$\sqrt{2}$=3$\sqrt{2}$,
故答案为:3$\sqrt{2}$.
点评 本题主要考查了轴对称-路径最短问题,用待定系数法求一次函数的解析式,熟练掌握利用对称轴求路径最短问题是解决问题的关键.

练习册系列答案
相关题目
5.三角形的一个外角小于与它相邻的内角,这个三角形是( )
| A. | 直角三角形 | B. | 钝角三角线 | C. | 锐角三角形 | D. | 不确定 |
6. 如图魔方共由多少个小正方体组成( )
如图魔方共由多少个小正方体组成( )
 如图魔方共由多少个小正方体组成( )
如图魔方共由多少个小正方体组成( )| A. | 18 | B. | 19 | C. | 26 | D. | 27 |
 细心观察图形,认真分析各式,然后解答问题:
细心观察图形,认真分析各式,然后解答问题: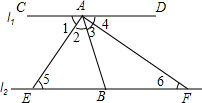 如图,已知直线l1∥直线l2,AE为∠CAB的角平分线,AF为∠DAB的角平分线,试说明:EB=BF.
如图,已知直线l1∥直线l2,AE为∠CAB的角平分线,AF为∠DAB的角平分线,试说明:EB=BF.