题目内容
4.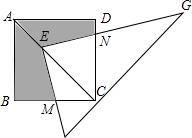 如图,点E在正方形ABCD的对角线AC上,且EC=2AE,Rt△FEG的两直角边EF、EG分别交BC、DC于点M、N.若正方形ABCD的边长为2,图中阴影部分的面积为( )
如图,点E在正方形ABCD的对角线AC上,且EC=2AE,Rt△FEG的两直角边EF、EG分别交BC、DC于点M、N.若正方形ABCD的边长为2,图中阴影部分的面积为( )| A. | 2 | B. | $\frac{4}{3}$ | C. | $\frac{16}{9}$ | D. | $\frac{20}{9}$ |
分析 过E作EP⊥BC于点P,EQ⊥CD于点Q,△EPM≌△EQN,利用四边形EMCN的面积等于正方形PCQE的面积求解,利用阴影部分的面积为=正方形ABCD的面积-四边形EMCN的面积计算即可.
解答 解:过E作EP⊥BC于点P,EQ⊥CD于点Q,
∵四边形ABCD是正方形,
∴∠BCD=90°,
又∵∠EPM=∠EQN=90°,
∴∠PEQ=90°,
∴∠PEM+∠MEQ=90°,
∵三角形FEG是直角三角形,
∴∠NEF=∠NEQ+∠MEQ=90°,
∴∠PEM=∠NEQ,
∵AC是∠BCD的角平分线,∠EPC=∠EQC=90°,
∴EP=EQ,四边形PCQE是正方形,
在△EPM和△EQN中,
$\left\{\begin{array}{l}{∠PEM=∠NEQ}\\{EP=EQ}\\{∠EPM=∠EQN}\end{array}\right.$,
∴△EPM≌△EQN(ASA)
∴S△EQN=S△EPM,
∴四边形EMCN的面积等于正方形PCQE的面积,
∵正方形ABCD的边长为2,
∴AC=2$\sqrt{2}$,
∵EC=2AE,
∴EC=$\frac{4\sqrt{2}}{3}$,
∴EP=PC=$\frac{4}{3}$,
∴阴影部分的面积为=正方形ABCD的面积-四边形EMCN的面积=4-$\frac{16}{9}$=$\frac{20}{9}$.
故选:D.
点评 本题主要考查了正方形的性质及全等三角形的判定及性质,解题的关键是作出辅助线,证出△EPM≌△EQN.

练习册系列答案
相关题目
12. 如图,在梯形ABCD中,AD∥BC,AB=DC,BC-AD=AB,过D作DE∥AB交BC于E,则△DEC是( )
如图,在梯形ABCD中,AD∥BC,AB=DC,BC-AD=AB,过D作DE∥AB交BC于E,则△DEC是( )
 如图,在梯形ABCD中,AD∥BC,AB=DC,BC-AD=AB,过D作DE∥AB交BC于E,则△DEC是( )
如图,在梯形ABCD中,AD∥BC,AB=DC,BC-AD=AB,过D作DE∥AB交BC于E,则△DEC是( )| A. | 不等边三角形 | B. | 等边三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
19.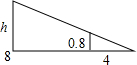 如图,小伟在打网球时,击球点距离球网的水平距离是8米.已知网高是0.8米,要使球恰好能打过网,且落在离网4米的位置,则球拍击打的高度h为( )
如图,小伟在打网球时,击球点距离球网的水平距离是8米.已知网高是0.8米,要使球恰好能打过网,且落在离网4米的位置,则球拍击打的高度h为( )
 如图,小伟在打网球时,击球点距离球网的水平距离是8米.已知网高是0.8米,要使球恰好能打过网,且落在离网4米的位置,则球拍击打的高度h为( )
如图,小伟在打网球时,击球点距离球网的水平距离是8米.已知网高是0.8米,要使球恰好能打过网,且落在离网4米的位置,则球拍击打的高度h为( )| A. | 1.0 | B. | 1.6 | C. | 2.0 | D. | 2.4 |
9. 如图,一个圆锥的母线长为6cm,底面圆的直径为8cm,则它的侧面展开扇形的圆心角度数是( )
如图,一个圆锥的母线长为6cm,底面圆的直径为8cm,则它的侧面展开扇形的圆心角度数是( )
 如图,一个圆锥的母线长为6cm,底面圆的直径为8cm,则它的侧面展开扇形的圆心角度数是( )
如图,一个圆锥的母线长为6cm,底面圆的直径为8cm,则它的侧面展开扇形的圆心角度数是( )| A. | 150° | B. | 240° | C. | 200° | D. | 180° |
16. 如图是一个正方体的展开图,将它折叠成正方体后,“我”字的对面是( )
如图是一个正方体的展开图,将它折叠成正方体后,“我”字的对面是( )
 如图是一个正方体的展开图,将它折叠成正方体后,“我”字的对面是( )
如图是一个正方体的展开图,将它折叠成正方体后,“我”字的对面是( )| A. | 校 | B. | 东 | C. | 母 | D. | 中 |
 如图是一个简单的数值运算程序,当输入的x的值为-2时,输出的值为9.
如图是一个简单的数值运算程序,当输入的x的值为-2时,输出的值为9.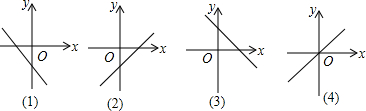

 如图,在Rt△ABC中,∠C=90°,BC=8cm,AC=6cm,点P从点A出发,沿AC向点C以1cm/s的速度运动,点Q从点C出发沿CB向点B以2cm/s的速度运动,过点P作PD∥BC,交AB于点D,点P、Q同时出发,当其中一个点停止运动时,另一个点也随之停止运动.设P、Q的运动时间为t(s)(0<t<4)
如图,在Rt△ABC中,∠C=90°,BC=8cm,AC=6cm,点P从点A出发,沿AC向点C以1cm/s的速度运动,点Q从点C出发沿CB向点B以2cm/s的速度运动,过点P作PD∥BC,交AB于点D,点P、Q同时出发,当其中一个点停止运动时,另一个点也随之停止运动.设P、Q的运动时间为t(s)(0<t<4)