题目内容
14.已知正△ABC的边长为6,那么能够完全覆盖这个正△ABC的最小圆的半径是2$\sqrt{3}$.分析 能够完全覆盖这个正△ABC的最小圆的半径是△ABC外接圆的半径,求出△ABC外接圆的半径即可解决问题.
解答 解:如图,那么能够完全覆盖这个正△ABC的最小圆的半径就是△ABC外接圆的半径,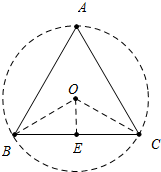
设⊙O是△ABC的外接圆,连接OB,OC,作OE⊥BC于E,
∵△ABC是等边三角形,
∴∠A=60°,∠BOC=2∠A=120°,
∵OB=OC,OE⊥BC,
∴∠BOE=60°,BE=EC=3,
∴sin60°=$\frac{BE}{OB}$,
∴OB=2$\sqrt{3}$,
故答案为2$\sqrt{3}$.
点评 本题考查等边三角形的性质、三角形外接圆的性质、锐角三角函数等知识,解题的关键是理解题意,学会转化的思想解决问题,属于中考常考题型.

练习册系列答案
相关题目
9.下列各式计算正确的是( )
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 4$\sqrt{3}$-3$\sqrt{4}$=1 | C. | 2$\sqrt{3}$×3$\sqrt{3}$=6 | D. | $\sqrt{27}$÷$\sqrt{3}$=3 |
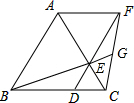 如图,已知△ABC是等边三角形,点D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF,CF,连接BE并延长交CF于点G.下列结论:
如图,已知△ABC是等边三角形,点D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF,CF,连接BE并延长交CF于点G.下列结论: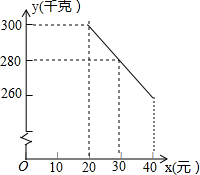 草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季,试销售成本为每千克20元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元,经试销发现,销售量y(千克)与销售单价x(元)符合一次函数关系,如图是y与x的函数关系图象.
草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季,试销售成本为每千克20元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元,经试销发现,销售量y(千克)与销售单价x(元)符合一次函数关系,如图是y与x的函数关系图象.
 如图,已知⊙O的直径AB=3cm,C为⊙O上的一点,sinA=$\frac{2}{5}$,则BC=$\frac{6}{5}$ cm.
如图,已知⊙O的直径AB=3cm,C为⊙O上的一点,sinA=$\frac{2}{5}$,则BC=$\frac{6}{5}$ cm.